Decision Tree 決策樹模型是一個不受資料分配限制的模型,模型結果以樹狀呈現,簡單易懂,解釋性極高,且模型同時兼具變數挑選與遺失值填補的機制,並能處理分類與回歸問題,是一個廣泛被使用的模型。另外,以決策樹為基礎集成學習而成的隨機森林,更能有效降低模型的錯誤率與並解決過度配適等問題的著名機器學習法之一。
Decision Tree 決策樹簡介
- 決策樹是一個多功能的機器學習演算法,不僅可以進行分類亦可進行回歸任務。
- 可以配適複雜的資料集,是個強大的演算法。
- 屬於無母數回歸方法(non-parametric):對資料長相的要求不像回歸模型(有母數法,parametric)嚴格,不需要假設資料的線性關係與常態分佈。
(無母數介紹請參考) - 決策樹演算法也是隨機森林演算法的基礎(隨機森林也是至今具潛力的演算法之一)。
- 有諸多演算法,常見的包括CART, CHAID。
- 決策樹可以用來建立非線性模型,通常被用在迴歸,也可以用在對於遞迴預測變數最二元分類。
補充-無母數統計:
- 適用於母體分佈情況未知、小樣本、母體分佈不為常態或不易轉換為常態,對資料長相的要求小。
- 無母數統計推論時所使用的樣本統計量分配通常與母體分配無關,不需要使用樣本統計量去推論母體中位數、適合度、獨立性、隨機性。
- 無母數統計又稱作「不受分配限制統計法」(distribution-free)。
常見的決策樹演算法比較
| 演算法 | 資料屬性 | 分割規則 | 修剪樹規則 |
| ID3 | 離散型 |
Entropy,
Gain Ratio
|
Predicted Error Rate |
| C4.5 | 離散型 | Gain Ratio | Predicted Error Rate |
| CHAID | 離散型 |
Chi-Square Test
|
No Pruning |
| CART | 離散與連續型 | Gini Index |
Entire Error Rate
(Training and Predicted)
|
決策樹挑選變數常用的測量值
常見的資訊量(衡量資料純度):
- Entropy (熵):
$$I_{H}(t)=-\sum_{i=1}^c p(i|t) \log_{2} p(i|t)$$
其中,H代表Homogeneity(同質性)。
當Entropy=0表示completely homogeneous(pure),而當Entropy=1則表示資料為50%-50%之組成,是不純的(impurity)。 - Gini Impurity (Gini不純度):
$$I_{G}(t) =\sum_{i=1}^c p(i|t)(1-p(i|t)) = 1-\sum_{i=1}^c p(i|t)^2$$
其中,G則代表Gini Impurity。
決定切割點的測量值:
- Information Gain (資訊增益): 則衡量節點切割前後資料純度的變化。節點的選擇,當選IG值越大的變數為佳。
$$IG = Info(D) – Info_{A}(D)$$
其中,\(Info(D)\)為原始資料純度,而\(Info_{\space A}(D)\)則表示使用A規則切割後的資料純度。
$$Info_{\space A}(D)=\sum_{j=1}^m \frac{N_{j}}{N_{p}} Info(D_{j})$$
當m=2,即為二元分類時,
$$IG = Info(D) – \frac{N_{left}}{N_{p}} Info(D_{left}) – \frac{N_{right}}{N_{p}} Info(D_{right})$$
資料與分析問題
- Data: 鐵達尼資料集包含13個變數與1309筆觀測值。
- Problem: 我們想分析與預測具有什麼樣特徵的乘客,比較有機會在冰山撞船後可以存活下來。
- Method: 使用CART(Classification and Regression Tree)決策樹模型來找出重要解釋變數。
訓練與視覺化決策樹,我們將進行以下步驟:
- 載入資料
- 資料探勘
- 資料前處理
- 產生訓練與測試資料集
- 建置模型
- 進行預測
- 衡量模型表現
- 修剪樹(Post-pruning)
- K-Fold Cross Validation
- 模型比較(1):條件推論樹(Conditional Inference Tree)
- 模型比較(2):隨機森林(Random Forest)
Step1: 載入資料
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# 從google drive shareable link 讀入csv檔案 # https://drive.google.com/file/d/1S7S-siBGkMR3YUVAbaTkfS1CxOji_Ngd/view?usp=sharing id inputData head(inputData) # pclass survived name sex age sibsp parch ticket fare # 1 1 1 Allen, Miss. Elisabeth Walton female 29.0000 0 0 24160 211.3375 # 2 1 1 Allison, Master. Hudson Trevor male 0.9167 1 2 113781 151.5500 # 3 1 0 Allison, Miss. Helen Loraine female 2.0000 1 2 113781 151.5500 # 4 1 0 Allison, Mr. Hudson Joshua Creighton male 30.0000 1 2 113781 151.5500 # 5 1 0 Allison, Mrs. Hudson J C (Bessie Waldo Daniels) female 25.0000 1 2 113781 151.5500 # 6 1 1 Anderson, Mr. Harry male 48.0000 0 0 19952 26.5500 # cabin embarked home.dest # 1 B5 S St Louis, MO # 2 C22 C26 S Montreal, PQ / Chesterville, ON # 3 C22 C26 S Montreal, PQ / Chesterville, ON # 4 C22 C26 S Montreal, PQ / Chesterville, ON # 5 C22 C26 S Montreal, PQ / Chesterville, ON # 6 E12 S New York, NY tail(inputData) # pclass survived name sex age sibsp parch ticket fare cabin embarked home.dest # 1304 3 0 Yousseff, Mr. Gerious male NA 0 0 2627 14.4583 C # 1305 3 0 Zabour, Miss. Hileni female 14.5 1 0 2665 14.4542 C # 1306 3 0 Zabour, Miss. Thamine female NA 1 0 2665 14.4542 C # 1307 3 0 Zakarian, Mr. Mapriededer male 26.5 0 0 2656 7.2250 C # 1308 3 0 Zakarian, Mr. Ortin male 27.0 0 0 2670 7.2250 C # 1309 3 0 Zimmerman, Mr. Leo male 29.0 0 0 315082 7.8750 S |
我們可以發現數據是經過排列過的,因為這樣會嚴重影響到我們後續隨機產生訓練與測試資料集,所以我們必須將資料重新隨機排列。
使用sample()隨機產生一組數列index。
|
1 2 |
shuffle_index head(shuffle_index) |
並將隨機數列index指派給titanic資料集。即可觀察到資料已無排序。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
inputData head(inputData) # pclass survived name sex age sibsp parch ticket fare cabin # 632 3 0 Andersson, Mr. Johan Samuel male 26 0 0 347075 7.775 # 526 2 0 Pain, Dr. Alfred male 23 0 0 244278 10.500 # 822 3 0 Goldsmith, Mr. Frank John male 33 1 1 363291 20.525 # 485 2 1 Lemore, Mrs. (Amelia Milley) female 34 0 0 C.A. 34260 10.500 F33 # 627 3 0 Andersson, Miss. Ida Augusta Margareta female 38 4 2 347091 7.775 # 1183 3 1 Salkjelsvik, Miss. Anna Kristine female 21 0 0 343120 7.650 # embarked home.dest # 632 S Hartford, CT # 526 S Hamilton, ON # 822 S Strood, Kent, England Detroit, MI # 485 S Chicago, IL # 627 S Vadsbro, Sweden Ministee, MI # 1183 S |
Step2: 資料探勘
使用summary()摘要基礎統計。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
summary(inputData) # pclass survived name sex age # Min. :1.000 Min. :0.000 Connolly, Miss. Kate : 2 female:466 Min. : 0.1667 # 1st Qu.:2.000 1st Qu.:0.000 Kelly, Mr. James : 2 male :843 1st Qu.:21.0000 # Median :3.000 Median :0.000 Abbing, Mr. Anthony : 1 Median :28.0000 # Mean :2.295 Mean :0.382 Abbott, Master. Eugene Joseph : 1 Mean :29.8811 # 3rd Qu.:3.000 3rd Qu.:1.000 Abbott, Mr. Rossmore Edward : 1 3rd Qu.:39.0000 # Max. :3.000 Max. :1.000 Abbott, Mrs. Stanton (Rosa Hunt): 1 Max. :80.0000 # (Other) :1301 NA's :263 # sibsp parch ticket fare cabin embarked # Min. :0.0000 Min. :0.000 CA. 2343: 11 Min. : 0.000 :1014 : 2 # 1st Qu.:0.0000 1st Qu.:0.000 1601 : 8 1st Qu.: 7.896 C23 C25 C27 : 6 C:270 # Median :0.0000 Median :0.000 CA 2144 : 8 Median : 14.454 B57 B59 B63 B66: 5 Q:123 # Mean :0.4989 Mean :0.385 3101295 : 7 Mean : 33.295 G6 : 5 S:914 # 3rd Qu.:1.0000 3rd Qu.:0.000 347077 : 7 3rd Qu.: 31.275 B96 B98 : 4 # Max. :8.0000 Max. :9.000 347082 : 7 Max. :512.329 C22 C26 : 4 # (Other) :1261 NA's :1 (Other) : 271 # home.dest # :564 # New York, NY : 64 # London : 14 # Montreal, PQ : 10 # Cornwall / Akron, OH: 9 # Paris, France : 9 # (Other) :639 |
使用str()查看資料結構。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
str(inputData) # 'data.frame': 1309 obs. of 12 variables: # $ pclass : int 3 2 3 2 3 3 1 3 3 2 ... # $ survived : int 0 0 0 1 0 1 1 0 1 1 ... # $ name : Factor w/ 1307 levels "Abbing, Mr. Anthony",..: 41 920 459 703 36 1068 864 949 1092 516 ... # $ sex : Factor w/ 2 levels "female","male": 2 2 2 1 1 1 1 2 1 1 ... # $ age : num 26 23 33 34 38 21 23 NA NA 7 ... # $ sibsp : int 0 0 1 0 4 0 1 0 0 0 ... # $ parch : int 0 0 1 0 2 0 0 0 0 2 ... # $ ticket : Factor w/ 929 levels "110152","110413",..: 453 194 584 767 468 410 574 415 388 783 ... # $ fare : num 7.78 10.5 20.52 10.5 7.78 ... # $ cabin : Factor w/ 187 levels "","A10","A11",..: 1 1 1 183 1 1 134 1 1 1 ... # $ embarked : Factor w/ 4 levels "","C","Q","S": 4 4 4 4 4 4 2 4 3 4 ... # $ home.dest: Factor w/ 370 levels "","?Havana, Cuba",..: 154 150 317 64 345 1 191 1 1 165 ... |
我們可初步發現:
- pclass(座艙等級)和survuved(生存與否)應由int轉換成factor變數
- 類別水準數過多的變數:name(1307 levels),ticket(929 levels), cabin(187 levels), home.dest(370 levels)應予以排除。
- 排除以上變數後,存在許多遺失值(NA value)的變數有:age(263), fare(1)。但由於CART決策樹rpart()演算法中,預設會刪除y遺失的資料列,並保留至少有一個預測變數未遺失的觀察資料列,並使用Surrogate Variables來預測遺失特徵值。因此我們不會特別處理遺失值的部分。(*更多決策樹遺失值預測請參考tree surrogate in CART)
Step3: 資料前處理
根據資料探勘結果,要處理的項目如下:
- 移除變數name(1307 levels),ticket(929 levels), cabin(187 levels), home.dest
- 將變數pclass(座艙等級)和survuved(生存與否)轉換為factor變數。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
library(dplyr) clean_inputData inputData %>% # Drop variables select(-c(home.dest, cabin, name, ticket)) %>% #Convert to factor level mutate(pclass = factor(pclass, levels = c(1, 2, 3), labels = c('Upper', 'Middle', 'Lower')), survived = factor(survived, levels = c(0, 1), labels = c('No', 'Yes'))) glimpse(clean_inputData) # Observations: 1,309 # Variables: 8 # $ pclass # $ survived # $ sex # $ age # $ sibsp # $ parch # $ fare # $ embarked |
Step4: 產生訓練與測試資料集
為了確保兩組資料集中生還比例不要差異太大,我們會先將資料依據目標變數(survived)分成兩組(No, Yes),再進行隨機切割成80%訓練組跟20%測試組。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
input_ones input_zeros set.seed(100) input_ones_training_row input_zeros_training_row training_ones training_zeros trainingData # 產生測試資料集 test_ones test_zeros testData |
檢查切割完的資料集大小與目標變數的分佈比例:
- 原始資料列1309被隨機切割為80%訓練資料集(1047筆)與20%測試資料集(262筆)。
- 發現訓練及測試資料集的目標變數survived比例都是38%。差異在1%以內。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
dim(trainingData) # [1] 1047 8 dim(testData) # [1] 262 8 # 確認兩資料是隨機的 prop.table(table(trainingData$survived)) # No Yes # 0.6179561 0.3820439 prop.table(table(testData$survived)) # No Yes # 0.6183206 0.3816794 |
Step5: 建置模型
我們使用CART(Classification and Regression Tree)決策樹演算法-rpart()。
- rpart為遞迴分割法(Recursive Partitioning Tree)的縮寫。
- 對所有參數和分割點進行評估。
- 最佳選擇是使分割後的組內資料更為「一致(pure)」。
- 「一致(pure)」是指組內資料的應變數取直變異較小。
- 使用Gini值測量資料的「一致(pure)」性(Homogeneity)。
- 建模過程分為兩階段(2 stages):
- 先長出最複雜的樹(grow the complex/full tree)。(直到Leaf size樹葉內的觀測個數少於5個或是模型沒有優化的空間為止)
- 再使用交叉驗證(Cross Validation)來修剪樹(Prune)。並尋找使估計風險值(estimate of risk)參數(complexity parameter)最小值的決策樹。
rpart()參數設定:
- method分成 “anova”、”poisson”、”class”和”exp”。當目標變數為factor時,我們將其設定為”class”。
- control: 通常會使用rpart.control()另外作設定(事前修樹,pre-prune)。
- na.action: 預設為na.rpart,即使用CART演算法中的surrogate variables做預測。
|
1 2 3 4 5 6 7 8 |
library(rpart) library(rpart.plot) fit # arguments: # method: # - "class" for a classification tree (y is a factor) # - "anova" for a regression tree |
使用rpart.plot()檢視決策樹規則。
|
1 |
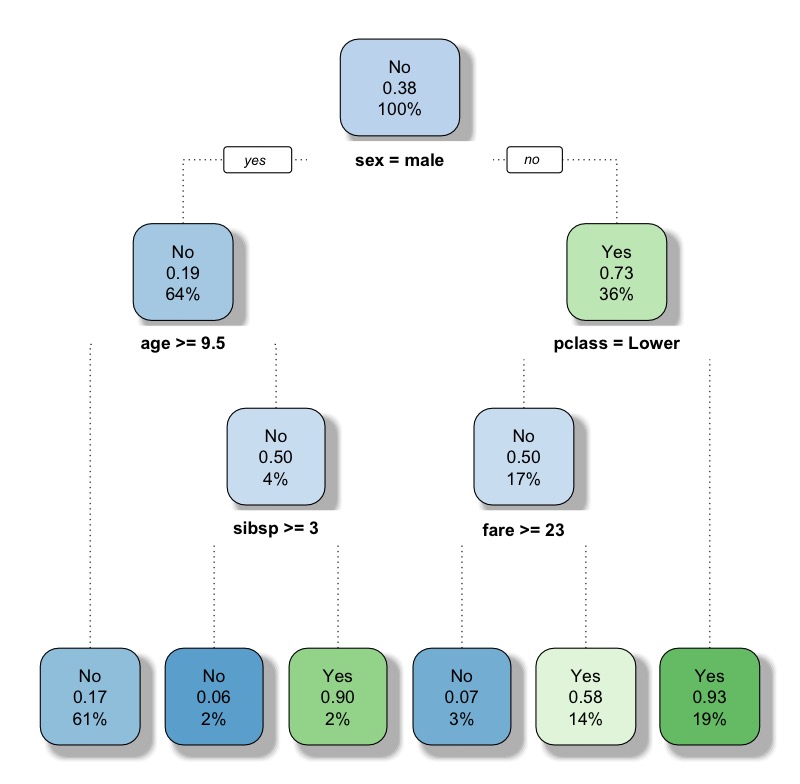
rpart.plot(fit, extra= 106) |
節點顏色越綠越深,代表該節點(條件下)的survived機率越高(目標事件發生機率越高)。
每個Node節點上的數值分別代表:
- 預測類別(0,1)
- 預測目標類別的機率(1的機率)
- 節點中觀測資料個數佔比
將決策樹規則使用rpart.rules()印出。
|
1 2 3 4 5 6 7 8 |
rpart.rules(x = fit,cover = TRUE) # survived cover # 0.06 when sex is male & age = 3 2% # 0.07 when sex is female & pclass is Lower & fare >= 23 3% # 0.17 when sex is male & age >= 9.5 61% # 0.58 when sex is female & pclass is Lower & fare # 0.90 when sex is male & age # 0.93 when sex is female & pclass is Upper or Middle 19% |
可發現規則依照survived比例(目標事件發生機率)由低到高排序。cover則代表該節點觀測資料個數占比。
檢視交叉驗證(cross-validation)的不同cp值(complexity parameter)下的錯誤率。
cp值代表的是每一個規則(切割)所能改善模型適合度的程度(cross validation relative error, or X-val relative error)。可以發現每一個新的規則的cp呈遞減趨勢。且rpart()預設cp=0.01,即代表如果該規則(切割)沒有達到至少0.01的模型適合度改善,則停止。(*rpart函數對complexity parameter的說明)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
printcp(x = fit) # Classification tree: # rpart(formula = survived ~ ., data = trainingData, method = "class") # # Variables actually used in tree construction: # [1] age fare pclass sex sibsp # # Root node error: 400/1047 = 0.38204 # # n= 1047 # # CP nsplit rel error xerror xstd # 1 0.425 0 1.000 1.000 0.039305 # 2 0.030 1 0.575 0.575 0.033492 # 3 0.020 3 0.515 0.530 0.032507 # 4 0.010 5 0.475 0.510 0.032040 |
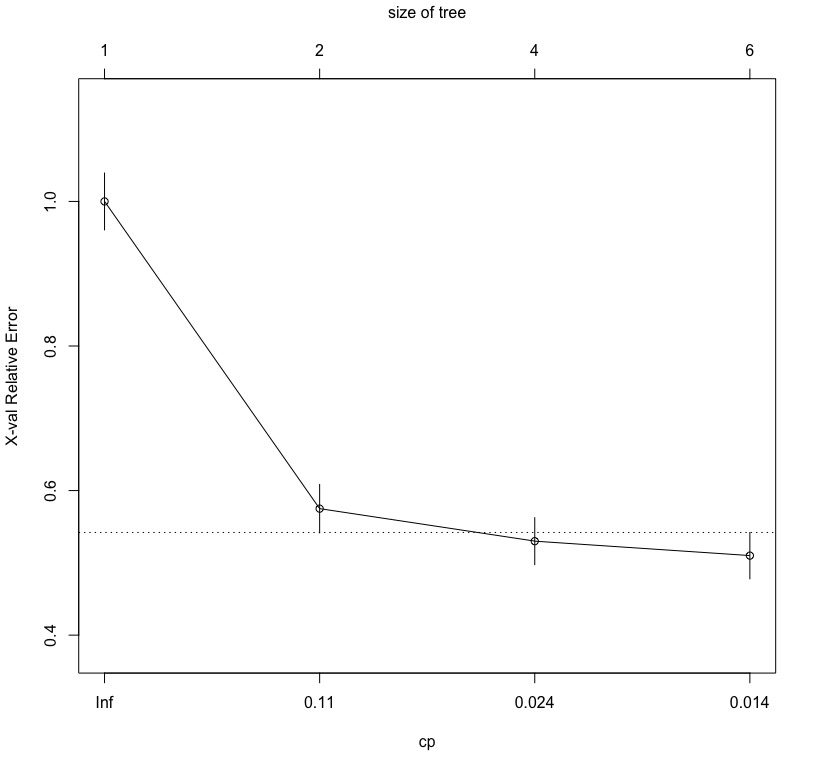
將模型的cp table畫出。可以觀察到,隨著模型的複雜度(成本)增加,所能改善的模型適合度的空間降低(X-val relative error)。
|
1 |
plotcp(x = fit) |
Step6: 進行預測
使用predict()將訓練好的模型套用在測試資料集上。
|
1 2 3 4 5 6 |
predicted # 參數說明: # type: Type of prediction # - 'class': for classification # - 'prob': to compute the probability of each class # - 'vector': Predict the mean response at the node level |
Step7: 衡量模型表現
由於預測結果為類別型(0,1),故我們以Confusion Matrix為基礎,來計算以下幾個常用指標:
- Accuracy/Misclassification Rate
- Precision
- Sensitivity(or Recall)
- Specificity
計算Confusion Matrix(數據左欄位預測值,上方列為真實值)
|
1 2 3 4 5 |
tbl tbl # predicted No Yes # No 140 28 # Yes 22 72 |
計算模型的正確率Accuracy
|
1 2 3 4 |
# Accuracy accuracy accuracy # [1] 0.8091603 |
可以發現未修剪的模型對測試資料的預測正確率高達近81%。
Step8: 修剪樹(Post-Pruning)
一般來說,修剪樹可以分為事前與事後。
- 事前:透過rpart.control()來調整重要參數,包括:
- minsplit:每一個node最少要幾個觀測值,預設為20。
- minbucket:在末端的node上(Leaf,樹葉)最少要幾個觀測值,預設為round(minsplit/3)。
- cp:complexity parameter。決定當新規則加入,改善模型相對誤差(x-val relative value)的程度如沒有大於cp值,則不加入該規則。預設為0.01。
- maxdepth:決策樹的深度,建議不超過6層。
- 事後:則是透過prune(x = , cp = )來設定。
我們這邊採用post-pruning法。並選擇讓交叉驗證中相對誤差改變量最小的cp值。
|
1 2 |
# prune tree : fit.prune |
將依據cp門檻值修剪後的樹規則繪出。
|
1 2 |
# plot the pruned tree rpart.plot(fit.prune, extra= 106, tweak = 1.1, shadow.col = "gray", branch.lty = 3, roundint = TRUE) |
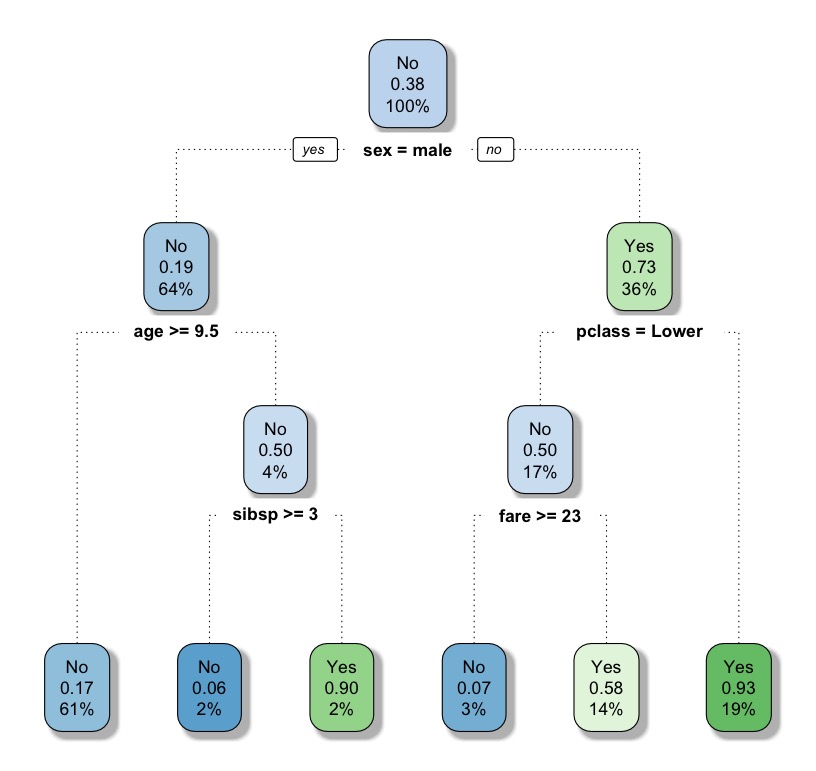
查看prune tree預測正確率。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
tbl_prune tbl_prune # actuals # predicted No Yes # No 140 28 # Yes 22 72 # Accuracy accuracy accuracy # [1] 0.8091603 |
可以發現pruned tree 和full tree兩者長得一樣,Accuracy也相同。原因在於,因為在建立full tree時,預設cp=0.01,跟prune()使用的cp值是相同的。
Step 9: K-Fold Cross Validation
為了確保模型無過度配適(overfitting)和預測準度的穩定性,我們使用k-fold cross validation(k=10)重新抽樣樣本進行模型驗證。理想中,交叉驗證後的平均正確率應與prune tree相近。
其中必須注意的是,因為資料中有遺失值觀測值,且train()函數中參數na.action預設值為na.fail(即遇到有遺失值程序會失敗),故必須將設定調整為na.pass(不採取任何動作)或na.omit(忽略有遺失值的觀測值),方能正常執行函數指令。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
library(caret) library(e1071) # 選則resampling的方法 train_control # specify the model train_control.model train_control.model # CART # # 1047 samples # 7 predictor # 2 classes: 'No', 'Yes' # # No pre-processing # Resampling: Cross-Validated (10 fold) # Summary of sample sizes: 943, 942, 942, 943, 942, 943, ... # Resampling results across tuning parameters: # # cp Accuracy Kappa # 0.020 0.8041850 0.5738715 # 0.030 0.7851282 0.5357307 # 0.425 0.6676099 0.1752418 # # Accuracy was used to select the optimal model using the largest value. # The final value used for the model was cp = 0.02. |
進行10次交叉驗證的平均正確率為80.4%,與修剪後的樹模型正確率80.91%沒有太大差異(差異百分比在1%以內)。表示模型沒有overfitting的問題。
如果將參數na.action調整為na.rpart(使用CART中的代理變數surrogate variables來預測)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
train_control.model.2 train_control.model.2 # CART # # 1047 samples # 7 predictor # 2 classes: 'No', 'Yes' # # No pre-processing # Resampling: Cross-Validated (10 fold) # Summary of sample sizes: 942, 943, 942, 943, 942, 942, ... # Resampling results across tuning parameters: # # cp Accuracy Kappa # 0.020 0.8042308 0.5735154 # 0.030 0.7880037 0.5452657 # 0.425 0.6685714 0.1862793 # # Accuracy was used to select the optimal model using the largest value. # The final value used for the model was cp = 0.02. |
進行10次交叉驗證的平均正確率亦約為80.4%。
Step 10: 模型比較(1)-條件推論樹(Conditional Inference Tree)
- R的party套件提供無母數回歸(non-parametric regression)樹模型,可處理名目(nominal)、尺度(ordinal)、數值(numeric)、設限(censored)、多變量(multivariate)資料型態。
- 你可以使用ctree(formula, data = )函數來產生分類或回歸樹模型,樹模型類型會根據目標變數型態而有所不同。
- ctree()透過統計檢驗來決定預測變數與分割點之選擇。
- 先假設所有預測變數與目標變數獨立(Null Hypothesis)。
- 進行卡方獨立檢定(Chi-Square Test)。
- 檢驗p-value小於threshold(ex: 0.05)則拒絕虛無假設,表示預測變數與目標變數具有顯著相關性,加入模型。
- 將相關性最強的變數選做第一次分割的變數。
- 繼續在各自子資料集進行分割變數計算與選擇。
- 因為樹是根據統計量顯著與否來判斷規則之必要性,因此與rpart()不同,ctree()是不需要剪枝的(prune)。
- 另參數na.action預設為na.pass (即不採取任何動作)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
library(party) fit_ctree plot(fit_ctree) predicted.ctree tbl_ctree tbl_ctree # actuals # predicted No Yes # No 140 29 # Yes 22 71 # Accuracy accuracy accuracy # [1] 0.8053435 |
可以發現模型準確率為80.5%,跟rpart演算法的k-fold交叉驗證的平均正確率80.4%沒有差太多。
Step 11: 模型比較(2)-隨機森林(Random Forest)
- 隨機森林是一個集成學習法(ensemble learning),意思是將幾個建立好的模型結果整合在一起,以提升預測準確率。
- 由集成學習法建立的模型較能不容易發生過度配適的問題,雖然提供較好的預測,但在推論和解釋度方面就會有所限制。
- 隨機森林由好幾個決策樹所組成,而不同決策樹是由不同隨機抽取的預測變數形成的。
- 而且特別的是,隨機森林不止對列(Row)進行抽樣,亦對行(Column)進行抽樣,因此所產生的子集資料,其實是行與列同時抽樣後的結果。
- 對列抽樣,可以部分解決因類別不平衡(Class Imbalance)對預測帶來的問題;而對行抽樣,則可解決部分因共線性(collinearity)對預測造成的問題。
(若是探討對「變數解釋性」的影響,則需要用 Lasso和Stepwise來解決)。 - 我們可用R裡面randomForest套件中的randomForest()函數來建立隨機森林。
- 參數na.action預設為na.fail (即遇到遺失值則停止執行)。因為資料集中有遺失觀測值,故必須將之調整為na.omit。
|
1 2 3 |
library(randomForest) set.seed(101) fit.rf |
檢視模型訓練結果。
- Number of trees: 隨機森林由500棵隨機生成的決策樹所組成。
- 利用OOB(Out Of Bag)運算出來的錯誤率為18.82%。
|
1 2 3 4 5 6 7 8 9 10 11 |
# Call: # randomForest(formula = survived ~ ., data = trainingData, na.action = na.omit) # Type of random forest: classification # Number of trees: 500 # No. of variables tried at each split: 2 # # OOB estimate of error rate: 18.82% # Confusion matrix: # No Yes class.error # No 463 44 0.08678501 # Yes 116 227 0.33819242 |
自己驗證與計算較精確的OOB estimate正確率Accuracy為81.17%。
|
1 2 3 4 |
tbl.rf accuracy accuracy # [1] 0.8117647 |
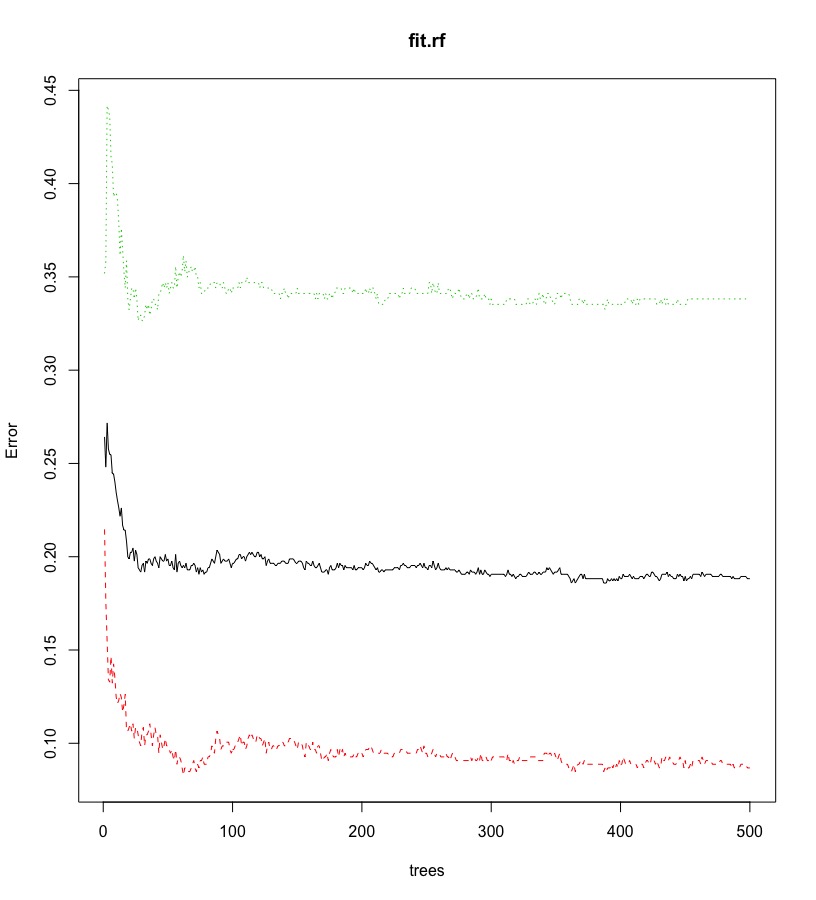
另外,我們將「增加每一顆決策樹,整體誤差的改變量」繪出,以輔助決策「需要多少顆決策樹,整體誤差才會趨於穩定」。
- 當為分類樹時(classification tree)
- 誤差為OOB(out-of-bag) Erro Rates。
- 黑色實線表示整體的OOB error rate,而其他顏色虛線表示各類別的OOB Error Rate。
- 當為回歸樹時(regression tree)
- 誤差為OOB(out-of-bag) MSE。
- 只會有一條黑色實線代表整體的OOB MSE。
|
1 |
plot(fit.rf) |
從圖中幾條線可以觀察到:
- 整體錯誤率(黑色實線)隨著決策樹數量上升,下降到約18%並趨於穩定。
- 實際類別為Yes的錯誤率(綠色虛線)隨著決策樹數量的上升,下降到約33.8%並趨於穩定。
- 實際類別為No的錯誤率(紅色虛線)隨著決策樹數量的上升,下降到約8.6%並趨於穩定。
- 而「最佳決策樹數目(ntree)」,約100多棵樹即足夠使誤差趨於穩定(不需要到500棵樹)。
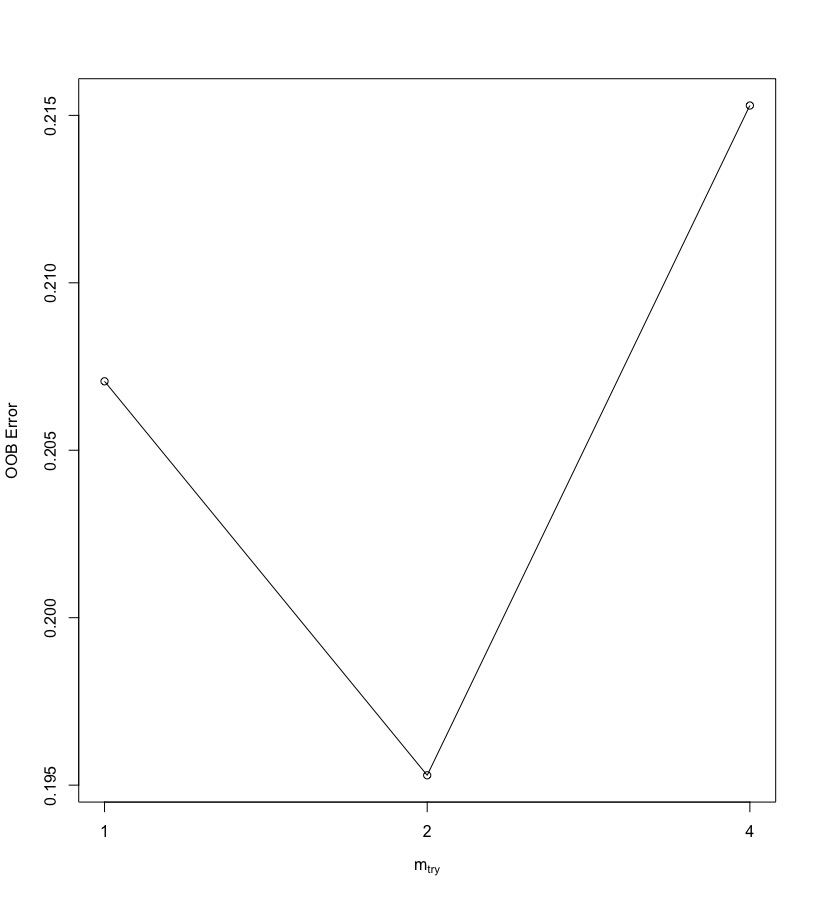
另外一個隨機森林中一個重要參數:mtry,表示每一個樹節點(node)在進行切割時(split)隨機抽樣的變數數量。可使用tuneRF()來調整mtry的值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
trainingData_naomit tuneRF(x = trainingData_naomit[,-2], y = trainingData_naomit[,2]) # mtry = 2 OOB error = 19.53% # Searching left ... # mtry = 1 OOB error = 20.71% # -0.06024096 0.05 # Searching right ... # mtry = 4 OOB error = 21.53% # -0.1024096 0.05 # mtry OOBError # 1.OOB 1 0.2070588 # 2.OOB 2 0.1952941 # 4.OOB 4 0.2152941 |
可以發現在mtry=2時,誤差最小。
randomForest中類別樹預設的mtry=sqrt(p),其中p代表x變數的數目。因為原始隨機森林模型預設值跟tuneRF建議的值相同,故我們另外不調整。
|
1 2 |
fit.rf$mtry # [1] 2 |
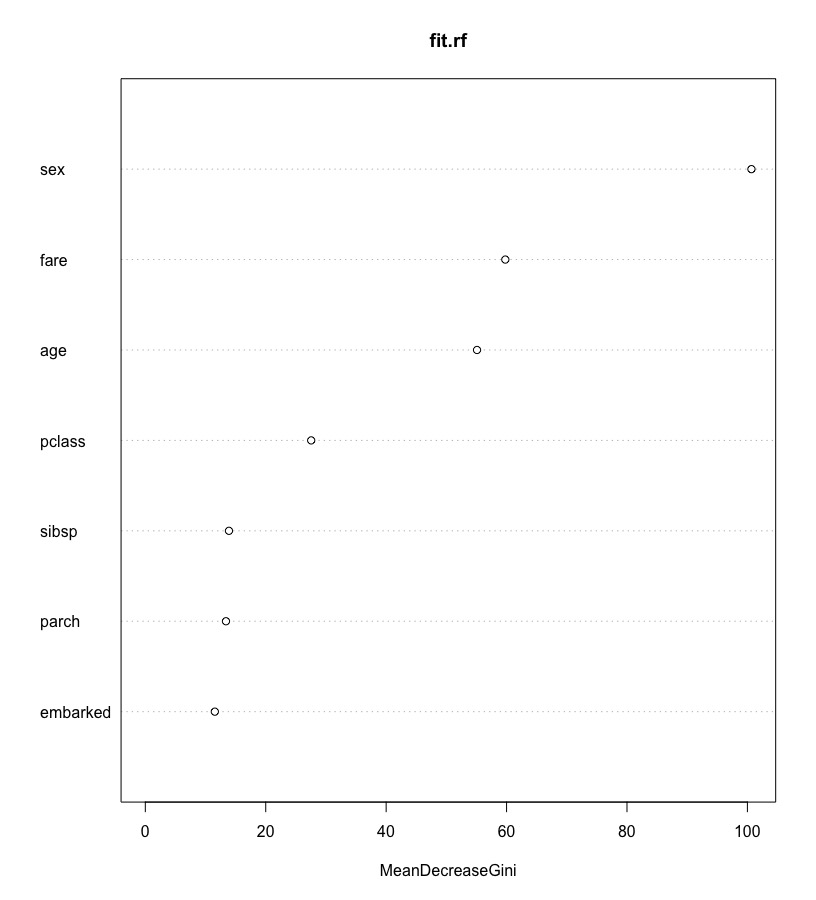
看每個x變數的重要性(the mean decrease in Gini index),即看哪個變數對損失函數Loss Function最有貢獻。(*randomForest參數importance預設值為False,僅會產生the mean decrease in Gini index,如果要產生其他指標如mean decrease in accuracy,要將其改為TRUE。)
|
1 2 3 4 5 6 7 8 9 10 11 12 |
round(importance(fit.rf),2) # importance of each predictor # or # round(fit.rf$importance, 2) # MeanDecreaseGini # pclass 27.55 # sex 100.67 # age 55.09 # sibsp 13.89 # parch 13.40 # fare 59.79 # embarked 11.55 |
將變數重要性(貢獻度)繪出。
|
1 |
varImpPlot(fit.rf) |
最後將調整好的模型應用在testData並評估正確性。
|
1 2 3 4 5 |
predicted.rf tbl.rf accuracy accuracy # [1] 0.8307692 |
隨機森林的預測準確率為83%,較原先的決策樹(accuracy = 80%)改善約4%。
總結
- Decision Tree 決策樹模型具有簡單易懂的樹狀邏輯圖,可解釋度高。
- Decision Tree 決策樹對於資料的要求低,沒有常態分配與線性關係的假設,不受資料分配限制。
- Decision Tree 決策樹的有變數篩選機制。
- rpart演算法進行Gini Index檢定,並計算complexity parameter來進行變數篩選。
- ctree演算法進行chi-square檢定,檢驗各投入變數是否與目標變數相關並計算p-value來看相關性的顯著效果。
- Decision Tree 決策樹亦有空值填補機制 – tree surrogate。
- rpart演算法na.action預設為na.rpart。(更多有關決策樹遺失值預測請參考 tree surrogate in CART)
- ctree演算法na.action預設為na.pass,可以將其改為na.rpart。
- Decision Tree 演算法rpart和ctree皆能處理連續型(continuous)與類別型(categorical)變數之切割。
- 由Decision Tree 決策樹衍伸出的集成學習法「隨機森林 random forest」可以有效降低模型的錯誤率、解決過度配適、透過反覆抽樣解決類別不平衡與共線性問題。
更多統計模型筆記連結:
- Linear Regression | 線性迴歸模型 | using AirQuality Dataset
- Regularized Regression | 正規化迴歸 – Ridge, Lasso, Elastic Net | R語言
- Logistic Regression 羅吉斯迴歸 | part1 – 資料探勘與處理 | 統計 R語言
- Logistic Regression 羅吉斯迴歸 | part2 – 模型建置、診斷與比較 | R語言
- Regression Tree | 迴歸樹, Bagging, Bootstrap Aggregation | R語言
- Random Forests 隨機森林 | randomForest, ranger, h2o | R語言
- Gradient Boosting Machines GBM | gbm, xgboost, h2o | R語言
- Hierarchical Clustering 階層式分群 | Clustering 資料分群 | R統計
- Partitional Clustering | 切割式分群 | Kmeans, Kmedoid | Clustering 資料分群
- Principal Components Analysis (PCA) | 主成份分析 | R 統計
學習筆記參考連結: