Partitional Clustering, 切割式分群,屬於資料分群屬的一種方法。資料分群屬於非監督式學習,所處理的資料是沒有正確答案/標籤/目標變數可參考的。常見的切割式分群演算法包括kmeans, kmedoid。本篇將介紹分「分割式分群法」的實作與特色。
資料分群簡介
- 資料分群是一個將資料分割成數個子集合的方法,主要目的包括:
- 找出資料中相近的群聚(clusters),
- 找出各群的代表點。代表點可以是群聚中的中心點(centroids)或是原型(prototypes)。
- 透過各群的代表點,可以達到幾個目標:
- 資料壓縮
- 降低雜訊
- 降低計算量
- 資料分群將依據資料自身屬性計算彼此間的相似度(物以類聚),而「相似度」主要有兩種型態:
- 「Compactness」:目標是讓子集合間差異最大化,子集合內差異最小化。如階層式分群和K-means分群。
- 「Connectedness」:目標是將可串連在一起的個體分成一群。如譜分群(Spectral Clustering)。
- 資料分群屬於非監督式學習法(Unsupervised Learning),即資料沒有標籤(unlabeled data)或沒有標準答案,無法透過所謂的目標變數(response variable)來做分類之訓練。也因為資料沒有標籤之緣故,與監督式學習法和強化式學習法不同,非監督式學習法無法衡量演算法的正確率。
資料分群系列文章會依序介紹以下幾種常見的分群方法:
- 階層式分群(hierarchical clustering)
- 聚合式階層分群法 Agglomerative Hierarchical Clustering
- 分裂式階層分群法 Divisive Hierarchical Clustering
- 最佳分群群數(Determining Optimal Clusters)
- 切割式分群(partitional clustering)
- K-means
- K-medoid
- 最佳分群群數(Determining Optimal Clusters)
- 譜分群(Spectral Clustering)
2.切割式分群(partitional clustering)
我們主要會cover以下步驟以完成K-Means & K-Medoid分群分析:
- Step 1: 載入所需套件(Packages)
- Step 2: 資料準備
- Step 3: 衡量群聚距離
- Step 4: K-Means分群
- Step 5: K-Medoid分群
- Step 6: 決定最適分群數目
- Elbow Method
- Average silhouette Width
- Gap Statistic
Step 1: 載入所需套件(Packages)
|
1 2 3 4 5 |
library(dplyr) library(magrittr) #pipelines library(tidyverse) # data manipulation library(cluster) # clustering algorithms library(factoextra) # clustering algorithms & visualization |
Step 2: 資料準備
我們使用R內建資料集USArrests。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 資料預處理:(1)遺失值處理(2)資料標準化(平均數為0,標準差為1) inputData USArrests %>% na.omit() %>% # 忽略遺失值 scale() # 資料標準化 head(inputData) # Murder Assault UrbanPop Rape # Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473 # Alaska 0.50786248 1.1068225 -1.2117642 2.484202941 # Arizona 0.07163341 1.4788032 0.9989801 1.042878388 # Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602 # California 0.27826823 1.2628144 1.7589234 2.067820292 # Colorado 0.02571456 0.3988593 0.8608085 1.864967207 |
Step 3: 衡量群聚距離
分類演算法將依據資料個體兩兩間之距離作為分群基礎。而不同距離衡量也將影響分類結果。我們根據不同距離定義計算所謂的「相異度/距離矩陣(dissimilarity/distance matrix)」,作為後續分類基礎。傳統計算距離常用的方法包括:(1)歐式距離(Euclidean Distance)(2)曼哈頓距離(Manhattan Distance)。定義分別如下:
歐式距離(Euclidean Distance)
$$d_{euc}(x,y)=\sqrt{\sum_{i=1}^n(x_{i}-y_{i})^2}$$
曼哈頓距離(Manhattan Distance)
$$d_{man}(x,y)=\sum_{i=1}^n|(x_{i}-y_{i})|$$
其中,x和y分別代表長度為n的向量。
幾個R裡面計算和視覺化資料個體間「相異度/距離矩陣」的函數包括:
- stat套件中的dist(method=…)函數:參數method預設為”euclidean”。其他可選擇的方法包括:”maximum”, “manhattan”, “canberra”, “binary”, “minkowski”。
- factoextra套件中的get_dist()函數:參數method預設為”euclidean”。和dist()函數不同的是,他支援correlation-based distance measures包括”pearson”, “kendall”和 “spearman” (*可根據資料屬性來選擇適合的距離計算方法,比如說,correlation-based distances常被運用在基因表達數據分析(gene expression data analyses))。
- factoextra套件中fviz_dist()函數:則可將相異度(距離)矩陣(使用get_dist()產生的物件)計算結果視覺化。
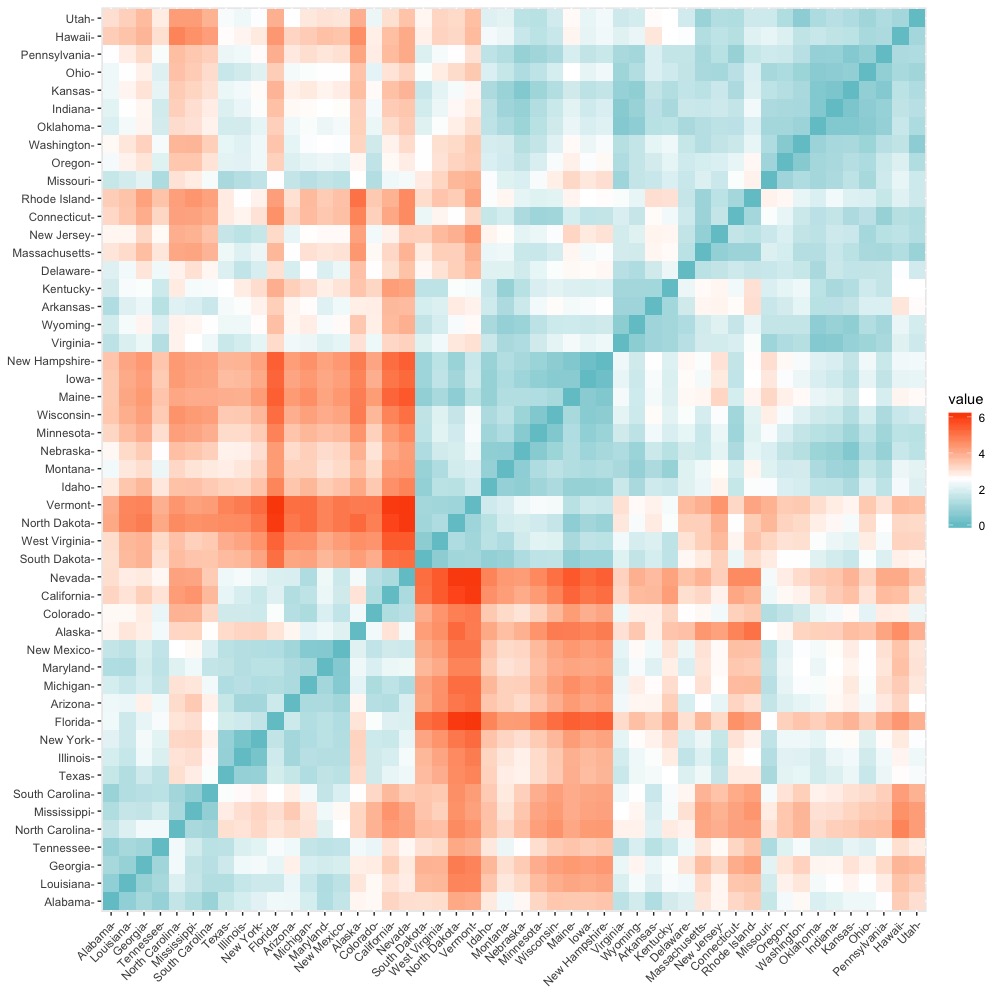
以下我們就使用get_dist()計算資料個體間兩兩距離(使用預設歐式距離法),並使用fviz_dist()將相異/距離矩陣結果視覺化。
|
1 2 |
distance fviz_dist(dist.obj = distance, gradient = list(low = "#00AFBB", mid = "white", high = "#FC4E07")) |
Step 4: K-Means分群
K-Means簡介
- 分群演算法中最出名的即為K-Means演算法。
- 是最簡單也最常使用的分群演算法。
- K-Means會根據一些距離的測量將觀測值分成數個組別。
- 需要事前指定分群數目。
- 目的是將極大化群內相似度,和最大化群間相異度。
- 指定群聚的平均值作為中心點(centroid)。
- 投入變數以連續變數為佳(kmeans(x = …只能為數值矩陣…))。
K-Means基礎概念
- 指定分群數k,並最小化k群組內變異總和(total intra-cluster variation or within-cluster variation)。
- K-Means的演算法有許多,而其中標準的演算法是由Hartigan教授所提出的。Hartigan教授將群聚內變異總和定義為:各資料點距離群中心的歐式距離平方加總。
$$W(C_{k})=\sum_{x_{i}\in C_{k}}(x_{i}-\mu_{k})^2$$
其中,- \(x_{i}\)代表群聚\(C_{k}\)中的資料點。
- \(\mu_{k}\)代表群聚\(C_{k}\)中資料點的平均值所指定的中心點。
- 而所有群內變異總和(total within-cluster variation)為:
$$total\space within-cluster\space variation\space = \sum_{i=1}^kW(C_{k})=\sum_{i=1}^k\sum_{x_{i}\in C_{k}}(x_{i}-\mu_{k})^2$$
total within-cluster variation是用來衡量群聚的緊緻度(Compactness),我們希望這個值越小越好。
K-Means演算法
- 由User事先指定分群數目k。
- 演算法隨機從資料集中挑選k個資料點當作初始中心點(initial centers)。
- 各資料點將依據距離初始中心的的歐式距離遠近分派指定給最近的群聚\(C_{k}\)(cluster assignment)。
- 各群聚\(C_{k}\)重新計算所有群聚中資料點的平均值作為新的中心點(centroid update)。並重新檢測所有資料點是否位在與其最近的中心點的群聚中。
- 重複第3~4步驟,來最小化各群聚的變異總和,直到各群聚組合趨於穩定與收斂(不再變動)(reach convergence),或已達最大迭代次數(R的kmeans函數預設為最大迭代次數為10)才停止。
使用R套件stats中的kmeans函數執行K-Means分群演算法
kmeans()函數幾個重要參數說明:
- centers: 指定分群數目k或指定初始中心點數目k。
- nstart: 因為初始中心點是隨機選取,所以可以透過nstart參數多嘗試幾組隨機初始值,並選擇回傳最好的初始中心點分群結果。
我們預設將資料分成2群(centers = 2),並隨機執行25次初始中心點挑選與分群結果。我們可以使用str()結構函數看分群結果回傳值。其中:
- $cluster表示資料被指定的分群結果。
- $center表示群聚中心點矩陣。
- $totss表示total sum of squares。
- $withininss: 表示within-cluster sum of squares,即單一群聚內總變異。
- $tot.withinss: 表示total within-cluster sum of squares,即所有群聚內變異加總(sum($withinss))。
- $size: 每群聚內資料個數。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
set.seed(101) k_clust str(k_clust) # List of 9 # $ cluster : Named int [1:50] 2 2 2 1 2 2 1 1 2 2 ... # ..- attr(*, "names")= chr [1:50] "Alabama" "Alaska" "Arizona" "Arkansas" ... # $ centers : num [1:2, 1:4] -0.67 1.005 -0.676 1.014 -0.132 ... # ..- attr(*, "dimnames")=List of 2 # .. ..$ : chr [1:2] "1" "2" # .. ..$ : chr [1:4] "Murder" "Assault" "UrbanPop" "Rape" # $ totss : num 196 # $ withinss : num [1:2] 56.1 46.7 # $ tot.withinss: num 103 # $ betweenss : num 93.1 # $ size : int [1:2] 30 20 # $ iter : int 1 # $ ifault : int 0 # - attr(*, "class")= chr "kmeans" |
或是將分群結果印出。可以分別得知以下資訊:
- 各群聚大小(資料個數)。
- 群聚在各維度的中心點(平均值)(2×4的矩陣)。
- 各資料列(列名稱)被分類到的群聚結果。
- 各群聚的變異總和。
- 可使用的成分(available components),即我們可以透過kmeans產生的物件+$…取得的資訊。比如說k_clust$cluster即得得到各列分群結果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
k_clust # K-means clustering with 2 clusters of sizes 30, 20 # # Cluster means: # Murder Assault UrbanPop Rape # 1 -0.669956 -0.6758849 -0.1317235 -0.5646433 # 2 1.004934 1.0138274 0.1975853 0.8469650 # # Clustering vector: # Alabama Alaska Arizona Arkansas California Colorado Connecticut Delaware # 2 2 2 1 2 2 1 1 # Florida Georgia Hawaii Idaho Illinois Indiana Iowa Kansas # 2 2 1 1 2 1 1 1 # Kentucky Louisiana Maine Maryland Massachusetts Michigan Minnesota Mississippi # 1 2 1 2 1 2 1 2 # Missouri Montana Nebraska Nevada New Hampshire New Jersey New Mexico New York # 2 1 1 2 1 1 2 2 # North Carolina North Dakota Ohio Oklahoma Oregon Pennsylvania Rhode Island South Carolina # 2 1 1 1 1 1 1 2 # South Dakota Tennessee Texas Utah Vermont Virginia Washington West Virginia # 1 2 2 1 1 1 1 1 # Wisconsin Wyoming # 1 1 # # Within cluster sum of squares by cluster: # [1] 56.11445 46.74796 # (between_SS / total_SS = 47.5 %) # # Available components: # # [1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" "size" # [8] "iter" "ifault" |
我們可以進一步使用factoextra套件中的fviz_cluster()函數來將分群結果視覺化。(*值得注意的是,當變數維度>2,fviz_cluster會使用主成分分析,找出最主要的兩個主成分來作為圖形的橫軸與縱軸。括號內的百分比則分別表示主成分解釋變異佔比。更多主成分分析PCA請參考「主成分分析(PCA)」)
|
1 |
fviz_cluster(k_clust, data = inputData) |
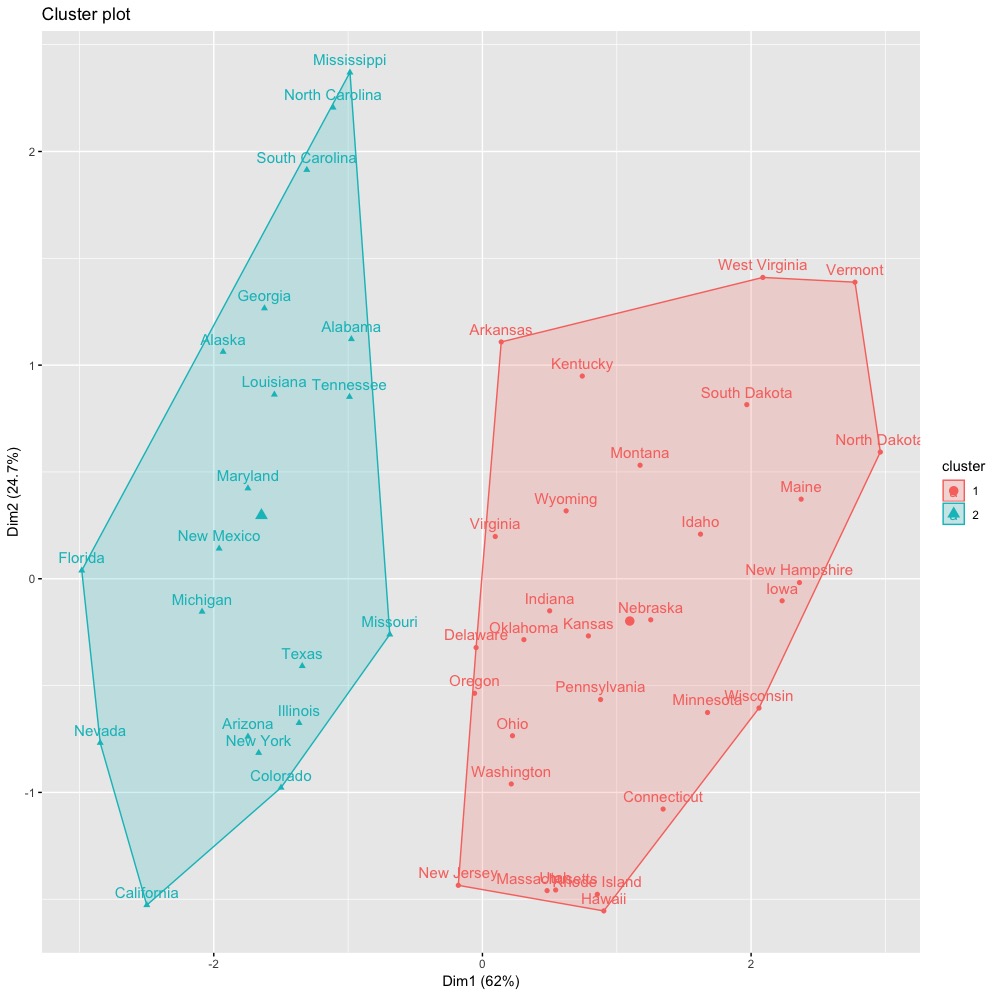
或者是,使用傳統的成對資料(分類結果,原始資料)繪製散佈圖來檢視分群結果。
|
1 2 3 4 5 6 7 |
inputData %>% as_tibble() %>% mutate(cluster = k_clust$cluster, #新增分群結果 state = row.names(USArrests) #將列名稱指定為原始資料標籤 ) %>% ggplot(aes(UrbanPop, Murder, color = factor(cluster), label = state)) + #使用ggplot套件繪圖(指定x,y軸),標記國家名稱,並依據分群結果上色 geom_text() |
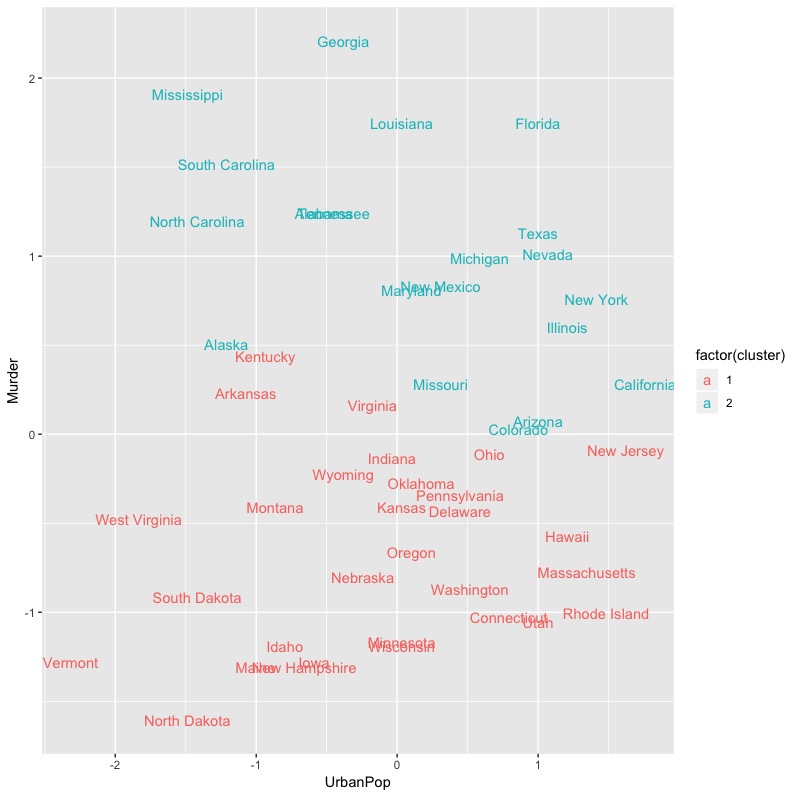
但因為通常資料維度會不止兩類,我們可以考慮使用useful套件中的plot.kmeans()函數,該函數可以將多維尺度調整以將資料投影到二維空間。然而這個效果似乎與factoextra套件中的fviz_cluster()函數無異,只不過還是factoextra套件中的fviz_cluster()函數更優!
|
1 2 |
library(useful) plot.kmeans(x = k_clust, data = inputData) |
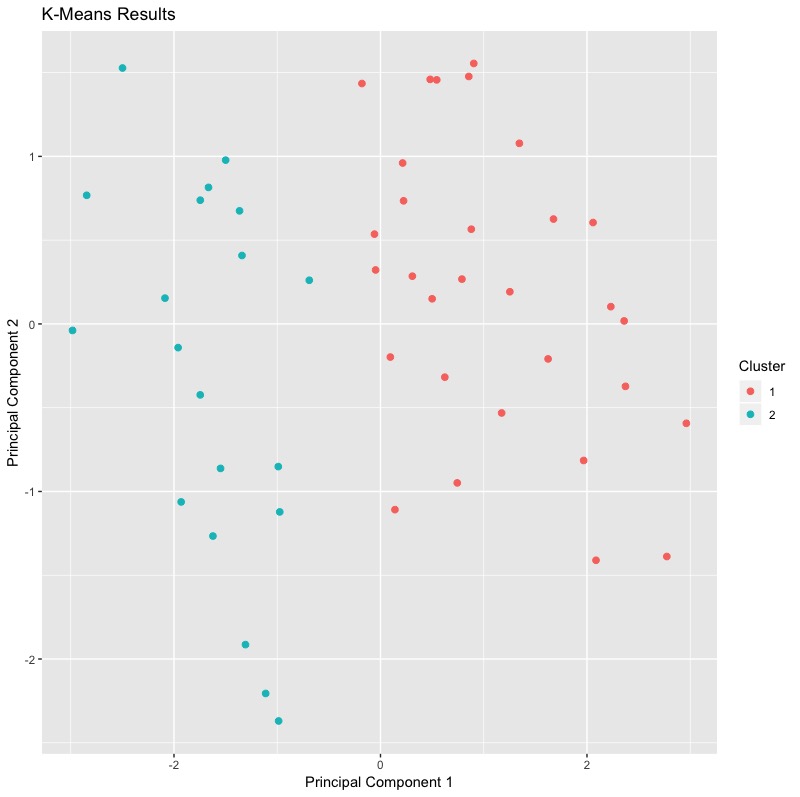
也因為我們一開始需要預設分群數目k值。我們打算試試不同初始中心點數目的效果差異。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 嘗試多種k的分群效果 set.seed(101) k_clust k_clust_3 k_clust_4 k_clust_5 # plots to compare p1 p2 p3 p4 library(gridExtra) grid.arrange(p1, p2, p3, p4, nrow = 2) # Arrange multiple grobs on a page (將不會影響到par()中參數設定) |
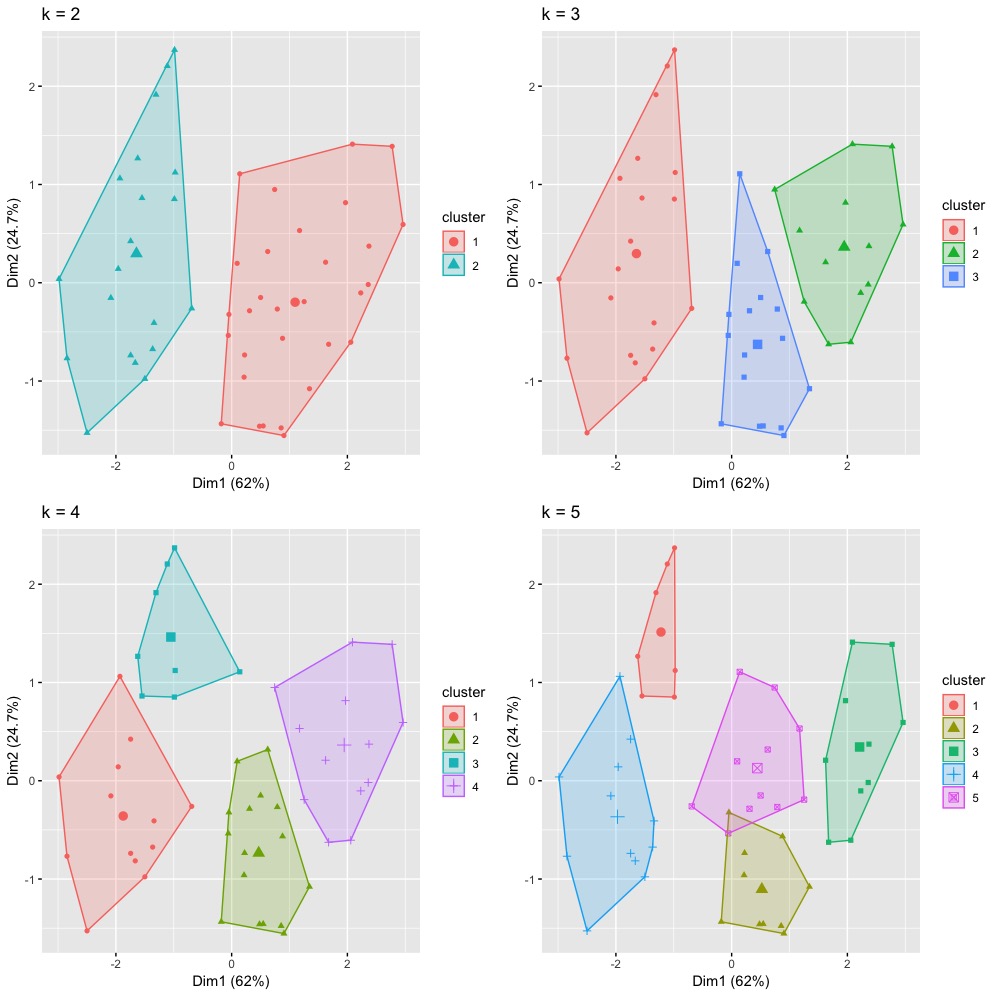
但僅憑上述嘗試,我們還是很難決定最佳群數該設定為多少。
Step 5: K-Medoid分群
(可以依情況決定是否將Step 4的kmeans()法取代)
- 使用K-Means演算法的兩個限制為:
- 不能處理類別變數資料 (kmeans(x = …只能為數值矩陣…))
- 容易受離群值影響
- 使用K-Mediods演算法時,中心點將選選擇群內某個觀測值,而非群內平均值,就像中位數一樣,較不易受離群值所影響。是K-Means更強大的版本。
- K-Medoids最常使用的演算法為PAM(Partitioning Around Medoid, 分割環繞物件法)。
- K-Medoids比K-Means更強大之處在於他最小化相異度加總值,而非僅是歐式距離平方和。(The goal is to find k representative objects which minimize the sum of the dissimilarities of the observations to their closest representative object. )
- 但遇到資料量較大時,K-Medoid法所需要的記憶體和運算時間都是龐大的,此時可以另外考慮clara(Clustering Large Applications)函數。
我們可以使用cluster套件中的pam()函數來執行。幾個重要參數包括:
- x: 可以為數值矩陣、data frame、甚是是相異度矩陣(dissimilarity matrix)。
- 若為numeric matrix or data frame須確保變數只能為數值。
- 若為dissimalirity matrix,可以是透過daisy()或dist()計算個體間距離的結果。
- 其中daisy()可以處理類別行變數的距離矩陣計算,須設定參數metric = c(“gower”)。
- 而傳統dist()則可以指定使用method = “euclidean” 或 “manhattan”。
- k: 指定分群數目。
- diss: TRUE/FALSE。投入的x是否為dissmilarity matrix。
- metric: 如果投入的x為matrix或data frame,需指定計算dissimilarity matrix所用的距離衡量方式,可為”euclidean” 或 “manhattan”。若投入的x已是dissimilarity matrix,則忽略該參數。
|
1 2 3 4 |
kmedoid.cluster # 分群結果視覺化 fviz_cluster(kmedoid.cluster, data = inputData,main = 'K-Medoid') |
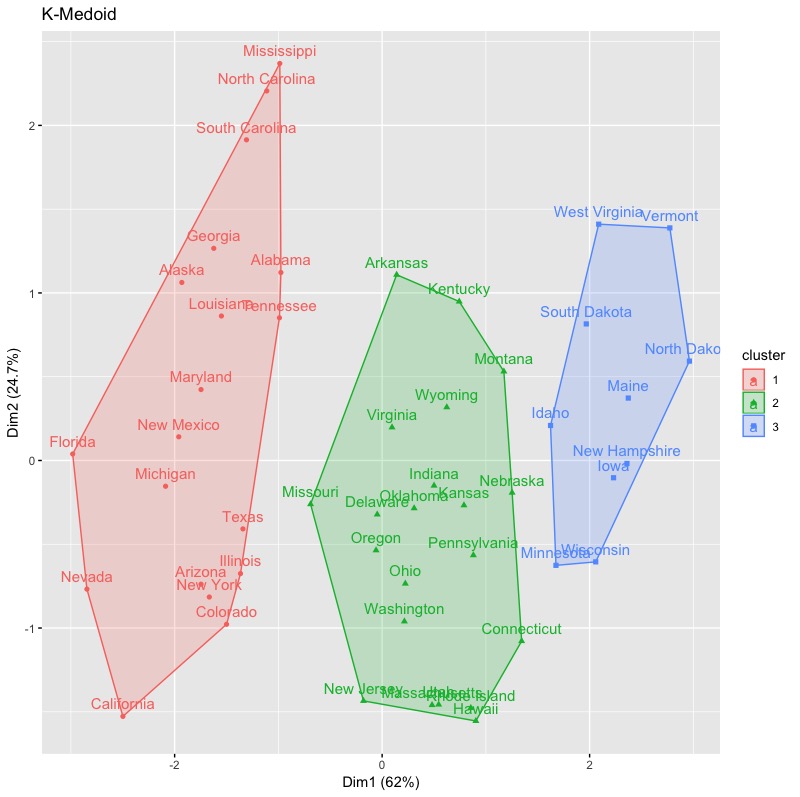
並且我們可以直接利用K-Medoid產生的物件繪製silhouette plot。
|
1 2 |
# 繪製側影圖 plot(kmedoid.cluster,which.plots = 2) |
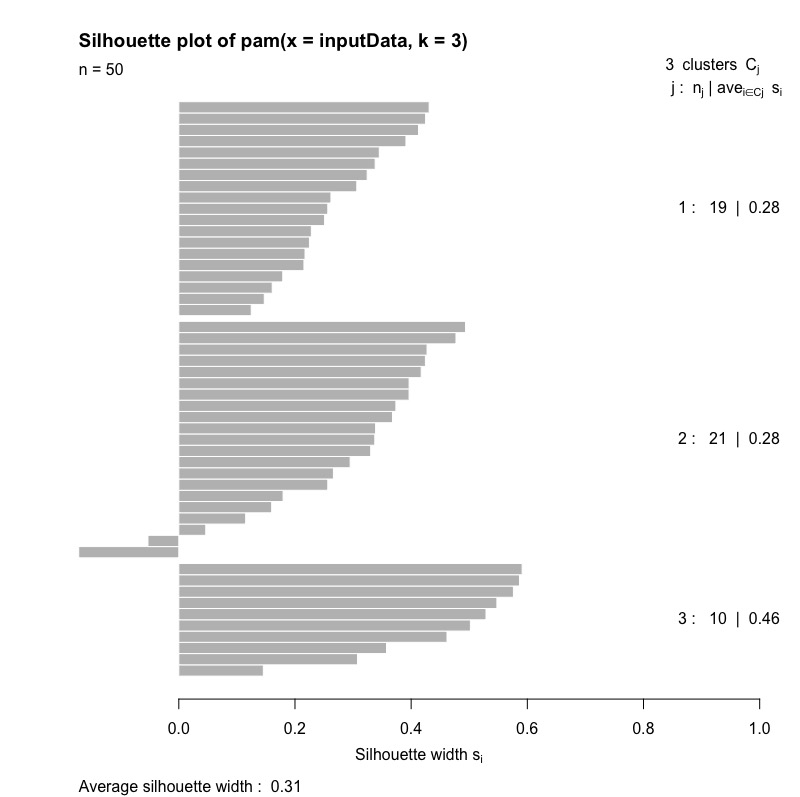
Step 6: 決定最適分群數目
以下為3個常見幫助我們決定最佳分群數的方法:
- Elbow Method(亦稱做Hartigan法)
- Average Silhouette method(側影圖法)
- Gap statistic(Gap統計量,預測-觀測)
Elbow Method
根據切割式分群的目的:最小化各群群內變異加總 (total within-cluster variation 或 total within-cluster sum of square,簡稱wss)。我們依序計算k = 1 ~ k=n各種分群結果的群內變異加總值,並將之與對應的k值繪製成圖(x軸為k值,y軸為wss)。並找出曲線彎曲(如膝蓋彎曲)處對應的k值,即各群群內變異加總值趨於收斂的轉折點,作為最佳的分群數目。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
set.seed(123) # function to compute total within-cluster sum of square wss kmeans( x = inputData, centers = k, nstart = 10 )$tot.withinss } # Compute and plot wss for k = 1 to k = 15 k.values # extract wss for 2-15 clusters wss_values plot(k.values, wss_values, type="b", pch = 19, frame = FALSE, xlab="Number of clusters K", ylab="Total within-clusters sum of squares") |
由下圖可觀察到,wss約在k=4時出現轉折彎曲,即wss下降幅度開始變小(趨於穩定)。
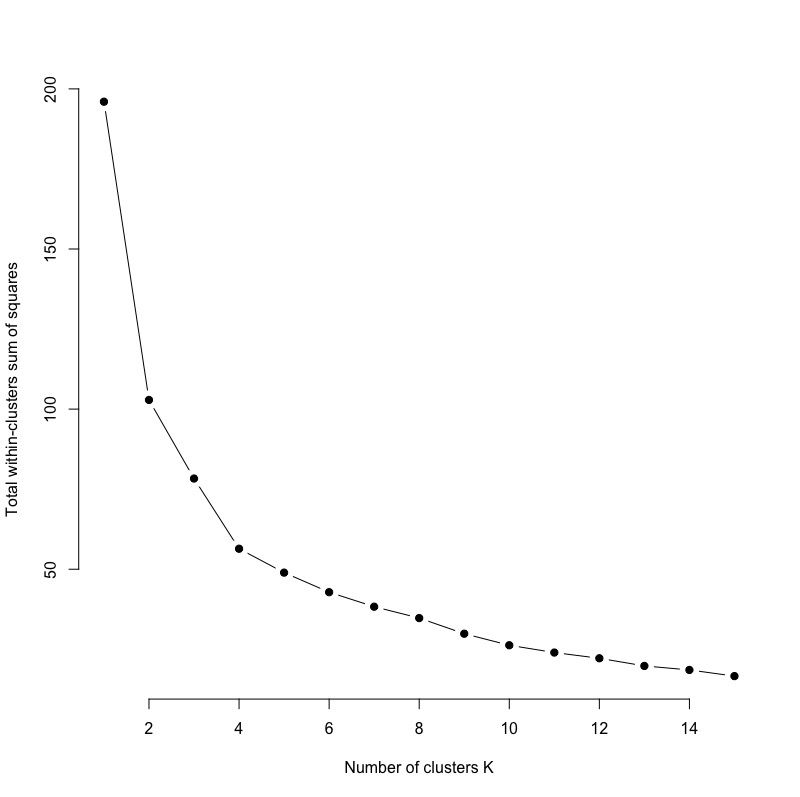
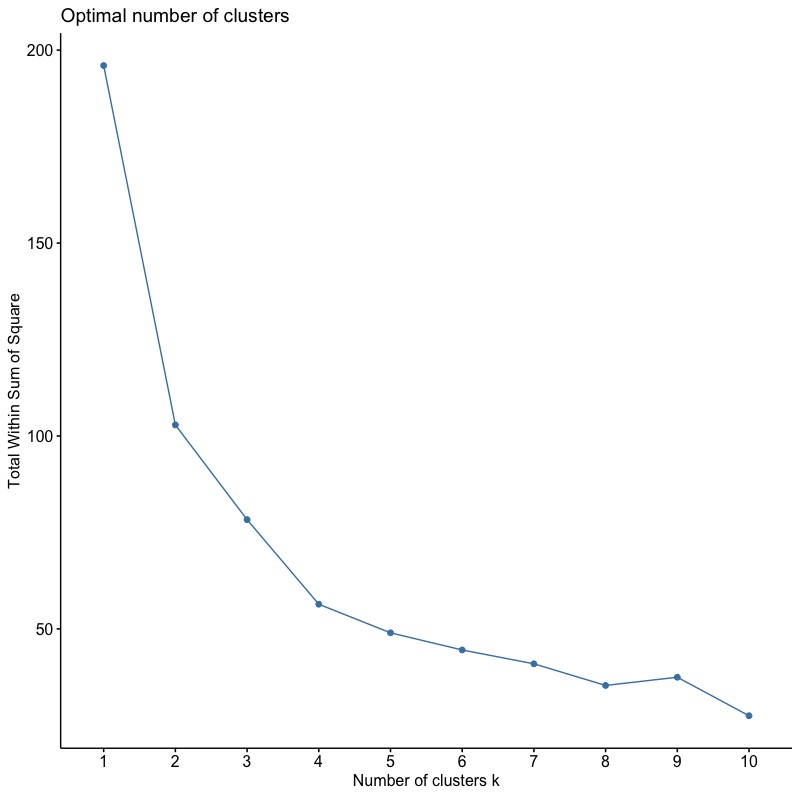
而幸好這樣複雜的計算與繪圖過程,我們都可以透過factoextra套件中的fviz_nbclust()函數來達成。便可將上述數行程式碼縮減到一行指令。
|
1 2 |
set.seed(123) fviz_nbclust(x = inputData,FUNcluster = kmeans, method = "wss") |
Average Silhouette Method
- 簡單來說,average silhouette method衡量各分群結果的品質 ((\(C_{1} \sim C_{k})\)都會有average silhouette width)。
- 該指標是透過計算各群聚中,各個物件的silhouette width,並取群內silhouette with平均值而得。
- 每一群聚中,各物件的silhouette with衡量的是該物件是否被很好的歸類在合適的群聚。
- 若silhouette with若為正數且值越大,則表示該觀測植被很好的分派到合適的群聚。
- 若silhouette with值很小或甚至為負數,則表示該觀測值的分群結果不是很合適。
- 整個群聚的average silhouette width則是將各觀測值的silhouette with取平均所計算而得。整個群聚的average silhouette with越大表示分群做得越好。
- 最後,再將所有k群聚的average silhouette with取平均,得出 每一個對應k群分群結果的average silhouette width。
- 於是我們可以得到k=1~k=n不同分群結果的average silhouette width。而其中極大化average silhouette width的k值即為最佳分群數目。
我們先來計算與視覺化,當k=5各群的average silhouette width以及整體分群結果的average silhouette width。
首先我們使用cluster套件中的silhouette()函數來計算每個觀測值得silhouette width。(初始計算結果並沒有各群的平均silhouette with)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
km.res ss # cluster neighbor sil_width # [1,] 3 2 0.448730181 # [2,] 4 3 0.054455351 # [3,] 4 1 0.432969809 # [4,] 2 3 0.228329605 # [5,] 4 1 0.448896074 # [6,] 4 2 0.310290004 # [7,] 1 2 0.279323646 # [8,] 1 2 -0.026200144 # [9,] 4 3 0.246185137 # [10,] 3 4 0.426879411 # [11,] 1 2 0.254134176 # [12,] 5 2 0.239121931 # [13,] 4 1 0.260389832 # [14,] 2 1 0.364248885 # [15,] 5 2 0.512603957 # [16,] 2 1 0.260830275 # [17,] 2 5 0.305423442 # [18,] 3 4 0.375176086 # [19,] 5 2 0.548907843 # [20,] 4 3 0.073438587 # [21,] 1 2 0.425221521 # [22,] 4 3 0.408874055 # [23,] 5 2 0.140353445 # [24,] 3 2 0.522765736 # [25,] 2 4 0.143376681 # [26,] 2 5 0.121906504 # [27,] 2 5 0.083351231 # [28,] 4 3 0.427993699 # [29,] 5 2 0.545620065 # [30,] 1 2 0.331314848 # [31,] 4 3 0.317371390 # [32,] 4 1 0.361348047 # [33,] 3 2 0.430379777 # [34,] 5 2 0.548983948 # [35,] 1 2 -0.016788571 # [36,] 2 1 0.246846452 # [37,] 2 1 0.143477706 # [38,] 1 2 -0.007681734 # [39,] 1 2 0.341420835 # [40,] 3 2 0.566811560 # [41,] 5 2 0.424934521 # [42,] 3 2 0.226342361 # [43,] 4 3 0.178417378 # [44,] 1 2 0.296027252 # [45,] 5 2 0.430596483 # [46,] 2 1 0.436958480 # [47,] 1 2 -0.014964942 # [48,] 5 2 0.349650799 # [49,] 5 1 0.295667125 # [50,] 2 1 0.403192800 # attr(,"Ordered") # [1] FALSE # attr(,"call") # silhouette.default(x = km.res$cluster, dist = dist(inputData)) # attr(,"class") # [1] "silhouette" |
如果要計算整體分群結果的average silhouette width,我們可以將結果的第三欄取平均值。
|
1 2 |
mean(ss[, 3]) # [1] 0.3030781 |
如果想要計算與視覺化各群的average silhouette width,我們可以使用plot()函數。
|
1 |
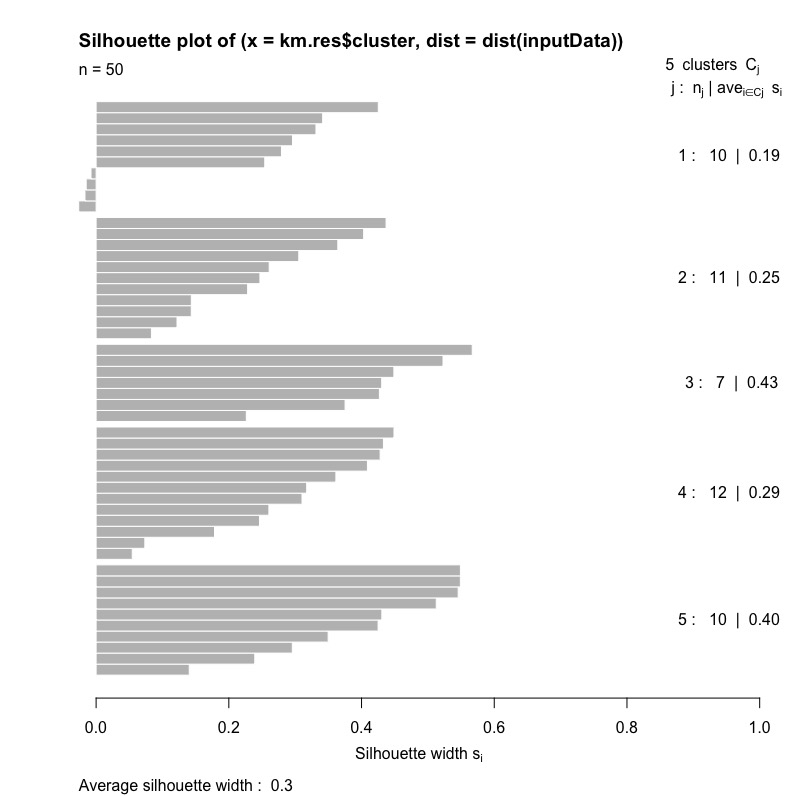
plot(ss) |
從下圖我們可以觀察到:
- j = 1 ~ 5。表示有五個群聚\(C_{j}\)。
- \(n_{j}\):各群觀測值數。
- \(ave_{i\in C_{j}}s_{i}\): 群聚\(C_{j}\)的average silhouette width。
- \(S_{i}\): 各觀測值的silhouette width。
- 圖最下方的average silhouette width則為整體分群結果的值。
有了以上單一k群結果的silhouette計算概念後,我們進一步比較不同k值(假設k=2 ~ 15)的分群結果品質。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# function to compute average silhouette for k clusters avg_sil km.res ss mean(ss[, 3]) } # Compute and plot wss for k = 2 to k = 15 k.values # extract avg silhouette for 2-15 clusters avg_sil_values plot(k.values, avg_sil_values, type = "b", pch = 19, frame = FALSE, xlab = "Number of clusters K", ylab = "Average Silhouettes") |
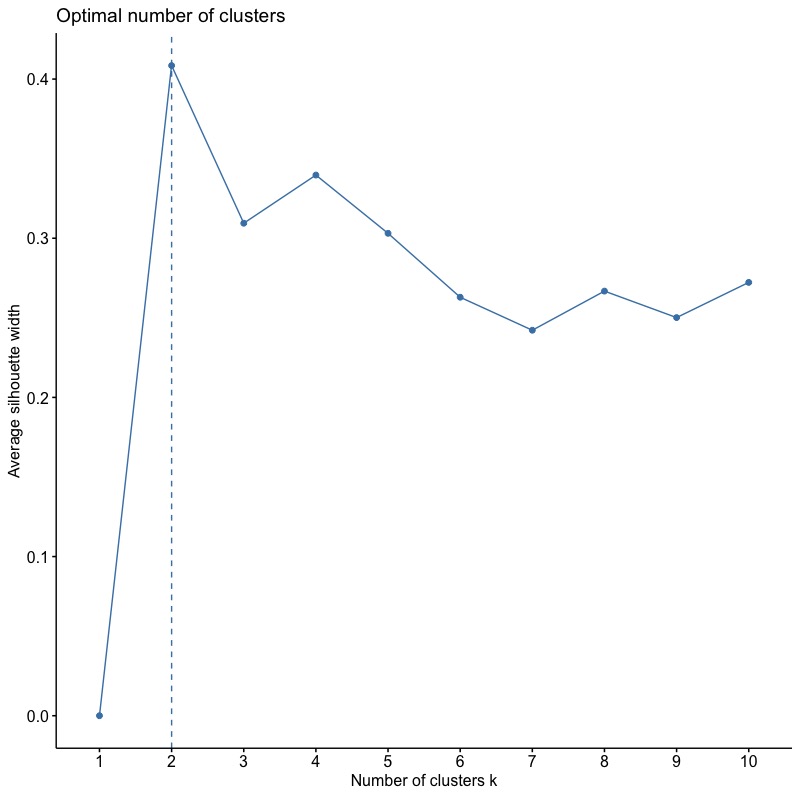
由下圖我們可以比較出,分兩群的結果最佳,分四群的結果次之。
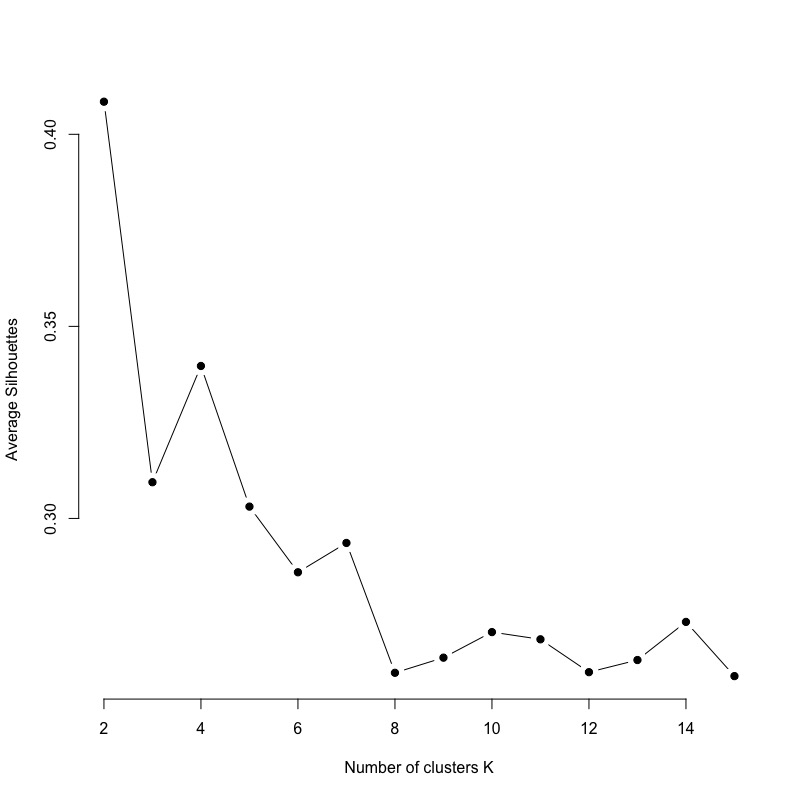
像Elbow Method一樣,我們也可以使用fviz_nbclust函數將上述結果的程式碼指令濃縮成一行並繪出。只需要將參數method從”wss“改成“silhouette“即可!
|
1 |
fviz_nbclust(inputData, kmeans, method = "silhouette") |
Gap statistic
- Gap Statistic法可以應用在任何分群演算法上(比如說分裂式分群或階層式分群)。
- Gap Statistic(k): 比較不同k水準值下,實際觀測值分群結果的群內總變異(\(W_{k}\))與自助抽樣法B回產生樣本分群結果期望群內總變異(\(\overline{W_{k}}\)),即衡量觀測和預期之間的差距。
- 群內總變異的期望值(\(\overline{W_{k}}\)): 使用自助抽樣法(Bootstap)進行B回重新抽樣,計算k水準值下重新抽樣樣本分群結果的群內總變異(\(W_{ki}\sim W_{kB}\)),並計算 k水準值下的群內總變異期望值,即
$$E(W_{k})=mean(W_{k})=\overline{W_{k}}=\frac{1}{B}\sum_{i=1}^B\log (W_{ki})$$ - 群內總變異的標準差Standard Deviation(\(Sd(W_{k})\)):
$$Sd(W_{k})=\sqrt{\frac{1}{B}\sum_{i=1}^B(\log (W_{ki}) – \overline{W_{k}})^2 }$$ - 群內總變異樣本平均值的標準誤Standard Error(\(s_{k}\)): 即樣本平均值(\(\overline{W_{k}}\))與真實母體平均值(\(\mu_{k}\))的變異。
$$s_{k} = sd(k)\times \sqrt{1+\frac{1}{B}}$$ - 自助抽樣將模擬蒙地卡羅的採樣過程,也就是說每一個變數\(x_{i}\),會依據他們的最大最小值範圍[\(\min(x_{i}),\max(x_{i})\)],來重新計算標準化後的值。
- Gap Statistic則是計算在不同k水準值下,觀測與預期值的總群內變異差異,公式如下:
$$Gap(k) =\overline{W_{k}} -{W_{k}}=\frac{1}{B}\sum_{i=1}^B\log (W_{ki}) – W_{k}$$ - 並且我們選擇使Gap(k)最大化的最小的k值,以符合:
$$Gap(k)\geq Gap(k+1)-s_{k+1}$$
即表示k群的分群結構和虛無假設的uniform分配(沒有分群)有很大的差距。
我們可以透過cluster套件中的clusGap()函數來計算不同k水平值對應的該統計量(Gap)以及標準誤(Standard Error, SE)。也因為我們要找到使最大化Gap(k)的最小k值,所以記得調整參數method=”firstmax”。將結果印出後,我們可看到每個對應k水平值的:
- logW: 觀測值群內總變異。
- E.logW: 群內總變異期望值。
- gap: E.logW – logW統計量。
- SE.sim: 標準誤(simulation standard error)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# compute gap statistic set.seed(123) gap_stat K.max = 10, B = 50) # Print the result print(gap_stat, method = "firstmax") # Clustering Gap statistic ["clusGap"] from call: # clusGap(x = inputData, FUNcluster = kmeans, K.max = 10, B = 50, nstart = 25) # B=50 simulated reference sets, k = 1..10; spaceH0="scaledPCA" # --> Number of clusters (method 'firstmax'): 4 # logW E.logW gap SE.sim # [1,] 3.458369 3.638250 0.1798804 0.03653200 # [2,] 3.135112 3.371452 0.2363409 0.03394132 # [3,] 2.977727 3.235385 0.2576588 0.03635372 # [4,] 2.826221 3.120441 0.2942199 0.03615597 # [5,] 2.738868 3.020288 0.2814197 0.03950085 # [6,] 2.669860 2.933533 0.2636730 0.03957994 # [7,] 2.598748 2.855759 0.2570109 0.03809451 # [8,] 2.531626 2.784000 0.2523744 0.03869283 # [9,] 2.468162 2.716498 0.2483355 0.03971815 # [10,] 2.394884 2.652241 0.2573567 0.04104674 |
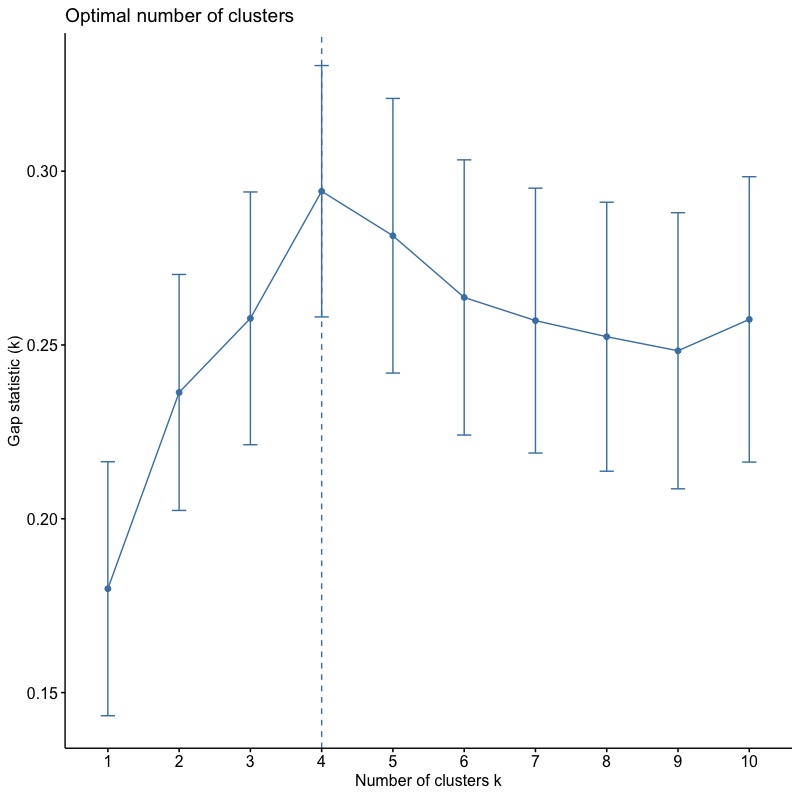
我們進一步使用fviz_gap_stat()函數將上面gap統計量計算結果視覺化。而根據Gap(k)統計量,最佳分群數為4組。
|
1 |
fviz_gap_stat(gap_stat) |
總結
- 影響切割式分群的幾個參數包括:隨機起始中心點的選擇、中心點定義、以及目標式最小化「距離」衡量定義。
- 中心點:
- kmeans的中心點是群內的平均值,易受離群值影響。
- kmedoid的中心點則是實際的點(類似中位數),不易受極端值影響。
- 目標式:
- kmeans是以最小化群內各點到中心點的「歐式距離」為目標
(minimize the sum of squared euclidean distances from points to the assigned cluster) - kmedoid是以最小化群內各點至中心點的「變異度」為目標
(minimize the sum of the dissimilarities of the observations to their closest representative object)
- kmeans是以最小化群內各點到中心點的「歐式距離」為目標
- 中心點:
- 因為切割式分群需使用者決定最適的群數,因此必須依據分群目的,綜合考量不同的方法(elbow method, average silhouette width, gap statistic)計算出的不同k值對應的組內變異加總值,來做決定。
- 由於目標式最小化的標的不同,雖然kmedoid效果會比kmeans更強大,但因為kmedoid需計算n^2的相異度矩陣,會耗費時間和運算記憶體,因此如果遇到大型數據時,可以使用clara()。pam()目前有觀測值上限(n <= 65536)。
更多統計模型筆記連結:
- Linear Regression | 線性迴歸模型 | using AirQuality Dataset
- Regularized Regression | 正規化迴歸 – Ridge, Lasso, Elastic Net | R語言
- Logistic Regression 羅吉斯迴歸 | part1 – 資料探勘與處理 | 統計 R語言
- Logistic Regression 羅吉斯迴歸 | part2 – 模型建置、診斷與比較 | R語言
- Decision Tree 決策樹 | CART, Conditional Inference Tree, Random Forest
- Regression Tree | 迴歸樹, Bagging, Bootstrap Aggregation | R語言
- Random Forests 隨機森林 | randomForest, ranger, h2o | R語言
- Gradient Boosting Machines GBM | gbm, xgboost, h2o | R語言
- Hierarchical Clustering 階層式分群 | Clustering 資料分群 | R統計
- Partitional Clustering | 切割式分群 | Kmeans, Kmedoid | Clustering 資料分群
- Principal Components Analysis (PCA) | 主成份分析 | R 統計