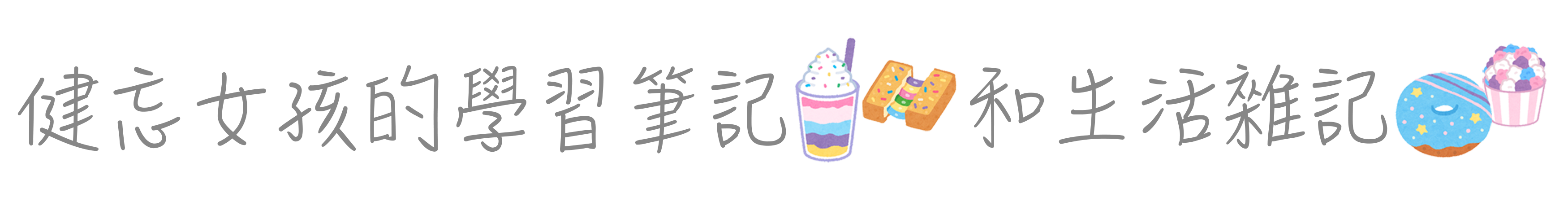主成份分析(principal components analysis, PCA)的應用非常廣泛,可以簡化資料維度資訊,用最精簡的主成份特徵來解釋目標變數的最大變異,避免共線性與過度配適等問題。而主成份分析的計算過程會使用到線性代數中的特徵值與特徵向量技術。本學習筆記會介紹主成份分析的基礎以及R套件的函數用法。
Principal Components Analysis 主成份分析簡介
- 主成分分析屬於非監督是式學習法,即處理一組沒有回應變數Y(目標變數)的一群X變數(\(X_{1},X_{2},…,X_{n}\)),即沒標籤的資料集(unlabeled data)。
- 主成份分析的主要目的為:降低資料維度。一方面可以避免共線性問題發生,一方面別是當資料維度非常大量時,可以減少運算並避免過度配適等問題產生。
本篇文章主要會分成以下幾個部分
- 載入所需套件
- 資料準備
- 主成份分析
- 萃取主成分
- R語言內建的PCA函數
1. 載入所需套件
|
1 2 |
library(tidyverse) # data manipulation and visualization library(gridExtra) # plot arrangement |
2. 資料準備
我們主要使用R內建數據USArrests。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
data("USArrests") head(USArrests, 10) # Murder Assault UrbanPop Rape # Alabama 13.2 236 58 21.2 # Alaska 10.0 263 48 44.5 # Arizona 8.1 294 80 31.0 # Arkansas 8.8 190 50 19.5 # California 9.0 276 91 40.6 # Colorado 7.9 204 78 38.7 # Connecticut 3.3 110 77 11.1 # Delaware 5.9 238 72 15.8 # Florida 15.4 335 80 31.9 # Georgia 17.4 211 60 25.8 |
3. Principal Components Analysis 主成份分析
- 目的為使用較少的變數來解釋最多的變異。
- 當遇上大量變數時,可以透過主成份分析將資料維度有效縮減,以利後續資料探勘與分析工作。
- 我們希望透過主成份分析來達成:運用最少的代表性資料維度來有效摘要大部分的資料資訊或變異(能捕捉到越多資料變異越好)。
principal components analysis 主成份分析計算
假設我們的dataset由n個觀測值和p個維度所組成,而主成份分析(PCA)所找出的維度將是p個維度的線性組合。
第一個主成份(\(Z_{1}\))到第p個主成份(\(Z_{p}\))可透過以下公式來表示:
$$Z_{1}=\phi_{11}X_{1}+\phi_{21}X_{2}+…+\phi_{p1}X_{p}$$
…
$$Z_{p}=\phi_{1p}X_{1}+\phi_{2p}X_{2}+…+\phi_{pp}X_{p}$$
其中,
- \(\phi_{ji}\)稱為每一個主成分\(Z_{i}\)的負荷向量(loading vector)(由\(\phi_{1i},\phi_{2i},…,\phi_{pi}\)所組成)。為標準化數值,不同主成分間的負荷向量可互相比較。
- 每個主成份\(Z_{i}\)的\(\phi_{ji}\)是透過最大化對應主成份\(Z_{i}\)的的解釋變異而得。
- \(\sum_{j=1}^p\phi_{ji}^2=1\),表示各主成分由不同比重的原始維度所組成。
- 每個主成分的負荷向量\(\phi_{ji}\)(loading vector)都是相互垂直的向量(\(\phi_{1}\perp \phi_{2} \perp …. \perp \phi_{p}\)),即表示各主成分彼此間的解釋變異為互相獨立的。
我們可以使用線性代數的技術來計算每一個主成分的負荷向量(loading vector):
- 資料標準化。
- 計算個原始維度兩兩間的共變異矩陣(covariance matrix)。其中,共變異數計算公式如下:
$$cov(X,Y)=\frac{1}{N-1}\sum_{i=1}^N(x_{i}-\bar{x})(y_{i}-\bar{y})$$ - 計算共變異矩陣的特徵值(eigenvalues)與特徵向量(eigenvectors)。而對應由大到小排列的特徵值的特徵向量,依序分別為解釋最大變異的主成分\(Z_{1}\)到解釋變異最小的主成分\(Z_{p}\)的負荷向量。
- 萃取主成分。
Step 1: 資料維度標準化
主成份分析的第一步就是進行資料的標準化,標準化的好處是,可以消除不同指標間的單位度量衡差異。待分析出不同主成份後,可以互相比較不同主成份間的平均值。我們將各維度(欄)進行標準化(centering)。*而scale的方式就是 (x – mean(x)) / sd(x)。
|
1 2 3 4 5 6 7 8 9 10 |
scaled_df head(scaled_df) # Murder Assault UrbanPop Rape # [1,] 1.24256408 0.7828393 -0.5209066 -0.003416473 # [2,] 0.50786248 1.1068225 -1.2117642 2.484202941 # [3,] 0.07163341 1.4788032 0.9989801 1.042878388 # [4,] 0.23234938 0.2308680 -1.0735927 -0.184916602 # [5,] 0.27826823 1.2628144 1.7589234 2.067820292 # [6,] 0.02571456 0.3988593 0.8608085 1.864967207 |
step 2: 我們可以使用cov()函數來計算兩兩變數的共變異數矩陣\(p\times p\)如下。
|
1 2 3 4 5 6 7 |
arrests.cov arrests.cov # Murder Assault UrbanPop Rape # Murder 1.00000000 0.8018733 0.06957262 0.5635788 # Assault 0.80187331 1.0000000 0.25887170 0.6652412 # UrbanPop 0.06957262 0.2588717 1.00000000 0.4113412 # Rape 0.56357883 0.6652412 0.41134124 1.0000000 |
step 3: 計算矩陣的特徵值(eigen values)與特徵向量(eigen vectors)。eigen()函數產出的物件包含兩部分:
- $values:排序過後的特徵值。
- $vectors:對應不同特徵值的特徵向量。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
arrests.eigen arrests.eigen # eigen() decomposition # $values # [1] 2.4802416 0.9897652 0.3565632 0.1734301 # # $vectors # [,1] [,2] [,3] [,4] # [1,] -0.5358995 0.4181809 -0.3412327 0.64922780 # [2,] -0.5831836 0.1879856 -0.2681484 -0.74340748 # [3,] -0.2781909 -0.8728062 -0.3780158 0.13387773 # [4,] -0.5434321 -0.1673186 0.8177779 0.08902432 |
step 4: 我們將萃取首兩大主成分1和主成分2作為我們說明的例子。
|
1 2 3 4 5 6 7 |
# Extract the loadings (phi # [,1] [,2] # [1,] -0.5358995 0.4181809 # [2,] -0.5831836 0.1879856 # [3,] -0.2781909 -0.8728062 # [4,] -0.5434321 -0.1673186 |
因為R計算的特徵向量預設為指向負值,且我們知道特徵向量是獨特的值,只要是在同一方向上,不管是正向還是負向純量縮放,都是相同的。為了方便說明,我們將特徵向量乘上純量-1。
|
1 2 3 4 5 6 7 8 9 |
phi row.names(phi) colnames(phi) phi # PC1 PC2 # Murder 0.5358995 -0.4181809 # Assault 0.5831836 -0.1879856 # UrbanPop 0.2781909 0.8728062 # Rape 0.5434321 0.1673186 |
檢視以上萃取的主成分向量,我們可以做出以下推論:
- 主成分1(PC1): 代表各大犯罪(包含謀殺、突擊、強姦)的犯罪發生率因子。
- 主成分2(PC2): 代表為城市化水平因子。
有了對主成分的基本了解後,我們將各觀測值投影到各主成分向量上,並計算各觀測值的各主成分分數(principal component scores)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# Calculate Principal Components scores PC1 PC2 # Create data frame with Principal Components scores PC head(PC) # State PC1 PC2 # 1 Alabama 0.9756604 -1.1220012 # 2 Alaska 1.9305379 -1.0624269 # 3 Arizona 1.7454429 0.7384595 # 4 Arkansas -0.1399989 -1.1085423 # 5 California 2.4986128 1.5274267 # 6 Colorado 1.4993407 0.9776297 |
接著,我們將各國對應的主成分維度繪製成二維的平面圖。
|
1 2 3 4 5 6 7 8 9 10 |
# Plot Principal Components for each State par(family="黑體-繁 中黑") ggplot(PC, aes(PC1, PC2)) + modelr::geom_ref_line(h = 0) + modelr::geom_ref_line(v = 0) + geom_text(aes(label = State), size = 3) + xlab("PC1: rate of serious crime, 重大犯罪發生率") + ylab("PC2: urbanization, 都市化程度") + ggtitle("First Two Principal Components of USArrests Data")+ theme(text=element_text(family="黑體-繁 中黑")) |
- 在PC1重大犯罪率維度上,Florida, Navada, California具有高重大犯罪率,而North Dakota, Vermont的重大犯罪率則較低。
- 在PC2都市化程度維度上,Hawaii, New Jersey為高度都市化城市,而North California, Mississippi的都市化程度則較低。
- 而接近中心點的城市如Indiana, Virginia則表示在兩維度表現皆為平均值。
4. 萃取主成分
透過以上計算過程我們能夠產出p個主成分向量,但是卻會有以下疑問:
- 該如何決定萃取的主成分數目?
- 萃取的主成分又構成資料變異的多少比例?
以下我們將介紹常用的指標PVE(The Proportion of Variance Explained)以及以利用該指標所繪出的資訊曲線圖,來輔助我們判斷每一個主成分解釋變異比例以及合適的萃取數。
The Proportion of Variance Explained (PVE)
第m個主成分解釋的變異量佔比計算公式如下:
$$PVE=\frac{\sum_{i=1}^n(\sum_{j=1}^p\phi_{jm}x_{ij})^2} {\sum_{j=1}^p\sum_{i=1}^n x_{ij}^2}$$
即為第m個主成分的特徵值除上所有主成分特徵值加總。
|
1 2 3 |
PVE round(PVE, 2) # [1] 0.62 0.25 0.09 0.04 |
從上面計算結果,我們可知第一個主成分解釋變異佔比為62%,第二主成分解釋變異占比為25%。而首兩個主成分總解釋變異便佔了87%。
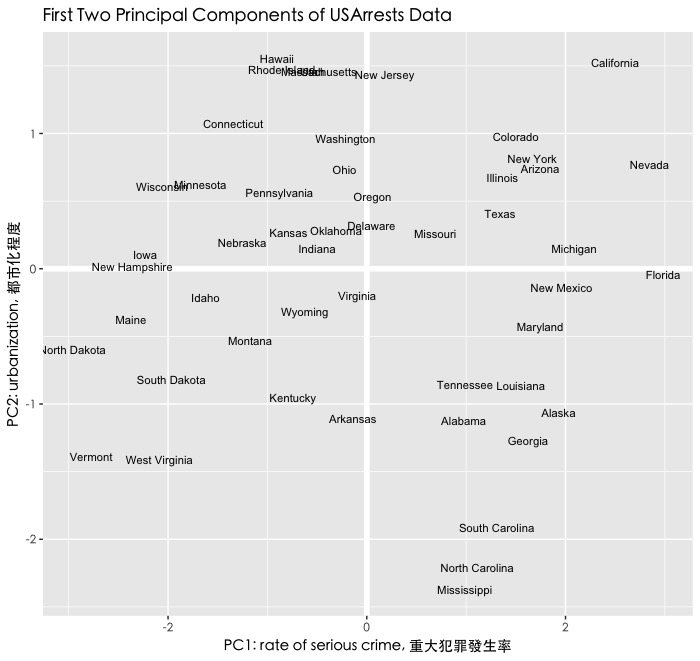
我們可繪出各主成分所對應的解釋變異佔比以及累積佔比圖。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# PVE (aka scree) plot PVEplot qplot(c(1:4), PVE) + geom_line() + xlab("Principal Component") + ylab("PVE") + ggtitle("Scree Plot") + ylim(0, 1) # Cumulative PVE plot cumPVE qplot(c(1:4), cumsum(PVE)) + geom_line() + xlab("Principal Component") + ylab(NULL) + ggtitle("Cumulative Scree Plot") + ylim(0,1) grid.arrange(PVEplot, cumPVE, ncol = 2) |
決定主成分萃取數
會視不同的分析目的和情形而定。一般來說,會根據每個主成分解釋變異百分比變化圖或累積圖,找出解釋絕大部分變異的最少主成分,約為線條出現「肘彎」轉折點處。比如說根據累積圖(上圖右),我們發現第三和第四主成分解釋的變異都有限,不如前兩個主成分,因此我們挑選解釋變異佔比前兩大主成分,兩主成分總構成約87%的變異。
5. R語言內建的PCA函數
在前面幾個步驟,我們為了熟悉主成分的計算邏輯,手動計算資料的共變異矩陣與矩陣對應的特徵值與特徵向量,但並不適合複雜的PCA運算。這邊將介紹一個R簡化PCA運算常用的套件: stats套件中的prcomp()函數。
prcomp()函數可以被用來快速處理上述幾個PCA相關運算。幾個重要參數包括:
- center: 預設值為TRUE。表示將資料平均值置中為0。
- scale: 預設值為TRUE。表示將資料標準差壓縮為1。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
pca_result pca_result # Standard deviations (1, .., p=4): # [1] 1.5748783 0.9948694 0.5971291 0.4164494 # # Rotation (n x k) = (4 x 4): # PC1 PC2 PC3 PC4 # Murder -0.5358995 0.4181809 -0.3412327 0.64922780 # Assault -0.5831836 0.1879856 -0.2681484 -0.74340748 # UrbanPop -0.2781909 -0.8728062 -0.3780158 0.13387773 # Rape -0.5434321 -0.1673186 0.8177779 0.08902432 names(pca_result) # [1] "sdev" "rotation" "center" "scale" "x" |
我們可將pca_result結果全部列出或列出list名稱names(pca_result)或透過pca_result$xxx單獨呼叫list物件,對照了解以下資訊。
sdev: 表示每個主成分的標準差。
|
1 2 |
pca_result$sdev # [1] 1.5748783 0.9948694 0.5971291 0.4164494 |
rotation: 每個主成分的負荷向量(loading vector)。也因為R預設特徵向量指向負向,我們調整將特徵向量乘上純量-1。經調整後,便和我們先前手動計算的結果相同了。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
pca_result$rotation # PC1 PC2 PC3 PC4 # Murder -0.5358995 0.4181809 -0.3412327 0.64922780 # Assault -0.5831836 0.1879856 -0.2681484 -0.74340748 # UrbanPop -0.2781909 -0.8728062 -0.3780158 0.13387773 # Rape -0.5434321 -0.1673186 0.8177779 0.08902432 pca_result$rotation pca_result$rotation # PC1 PC2 PC3 PC4 # Murder 0.5358995 -0.4181809 0.3412327 -0.64922780 # Assault 0.5831836 -0.1879856 0.2681484 0.74340748 # UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773 # Rape 0.5434321 0.1673186 -0.8177779 -0.08902432 |
center, scale: 每一個主成分在資料標準化前的平均數與標準差。
|
1 2 3 4 5 6 |
pca_result$center # Murder Assault UrbanPop Rape # 7.788 170.760 65.540 21.232 pca_result$scale # Murder Assault UrbanPop Rape # 4.355510 83.337661 14.474763 9.366385 |
另外,我們也可以從結果取得每一個國家(每一個觀察值)的主成分分數。(但記得,如同特徵向量之處理,主成分分數也要乘上純量-1) 。
|
1 2 3 4 5 6 7 8 9 |
pca_result$x head(pca_result$x) # PC1 PC2 PC3 PC4 # Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581 # Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454 # Arizona 1.7454429 0.7384595 -0.05423025 0.826264240 # Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554 # California 2.4986128 1.5274267 -0.59254100 0.338559240 # Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164 |
如果要印出二維主成分圖,可以使用stat套件中的biplot()函數。常用參數包括:
- choice: 預設為使用第一和第二欄來繪製(choice = 1:2)。如果想要調整繪製x,y軸,比如說繪製第三和第四主成分則可將參數設定為choices = 3:4。
|
1 |
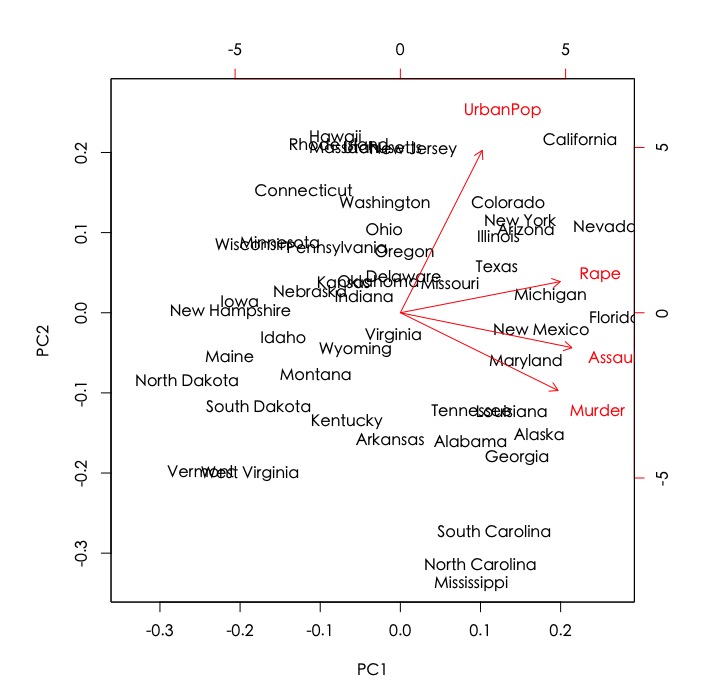
biplot(x = pca_result) #default為第一和第二欄 |
跟先前比較不同之處,圖中的標記的紅色向量分別表示各變數對主成分的作用的方向。
另外,我們也可以算出每個主成分解釋變異量。
|
1 2 |
(VE # [1] 2.4802416 0.9897652 0.3565632 0.1734301 |
計算PVE。結果跟先前手動計算相同。
|
1 2 3 |
PVE round(PVE, 2) ## [1] 0.62 0.25 0.09 0.04 |
總結
主成分分析的應用非常廣泛,不僅可搭配迴歸、羅吉斯回歸、分群演算法一併使用,來有效降低維度。
或是說,在查看分群結果時,我們可透過fviz_cluster()或plot.kmeans()函數將多維資料呈現在二維平面用的即是主成分分析方法(請參考「分群分析 Clustering | Partitional Clustering」)。
更多統計模型筆記連結:
- Linear Regression | 線性迴歸模型 | using AirQuality Dataset
- Regularized Regression | 正規化迴歸 – Ridge, Lasso, Elastic Net | R語言
- Logistic Regression 羅吉斯迴歸 | part1 – 資料探勘與處理 | 統計 R語言
- Logistic Regression 羅吉斯迴歸 | part2 – 模型建置、診斷與比較 | R語言
- Decision Tree 決策樹 | CART, Conditional Inference Tree, Random Forest
- Regression Tree | 迴歸樹, Bagging, Bootstrap Aggregation | R語言
- Random Forests 隨機森林 | randomForest, ranger, h2o | R語言
- Gradient Boosting Machines GBM | gbm, xgboost, h2o | R語言
- Hierarchical Clustering 階層式分群 | Clustering 資料分群 | R統計
- Partitional Clustering | 切割式分群 | Kmeans, Kmedoid | Clustering 資料分群
- Principal Components Analysis (PCA) | 主成份分析 | R 統計
參考: