Linear Regression 線性迴歸模型是用來預測連續型目標變數與預測變數間的線性關係,並存在許多資料符合常態分佈與線性關係等基本假設。預測變數可以是數值或類別型態,投入模型進行時類別變數都會被轉換成虛擬變數。對於有遺失值的觀測值則會直接忽略,且易受極端值影響,因此在使用模型前必須做好資料前處理。
Linear Regression Introduction
Linear Regression 線性迴歸模型主要是使用最適線性迴歸線來建立依變數Y和一個或多個自變數X間的關係,並可以此線性迴歸方程式,使用給定自變數X的值來預測依變數Y值(適用於目標變數為連續變數時,若目標變數為二元變數,則適用羅吉斯回歸)。(*線性迴歸方程式的建立則是使用最小平方法Least Sqaures Method來找尋X和Y之間的關係與趨勢)
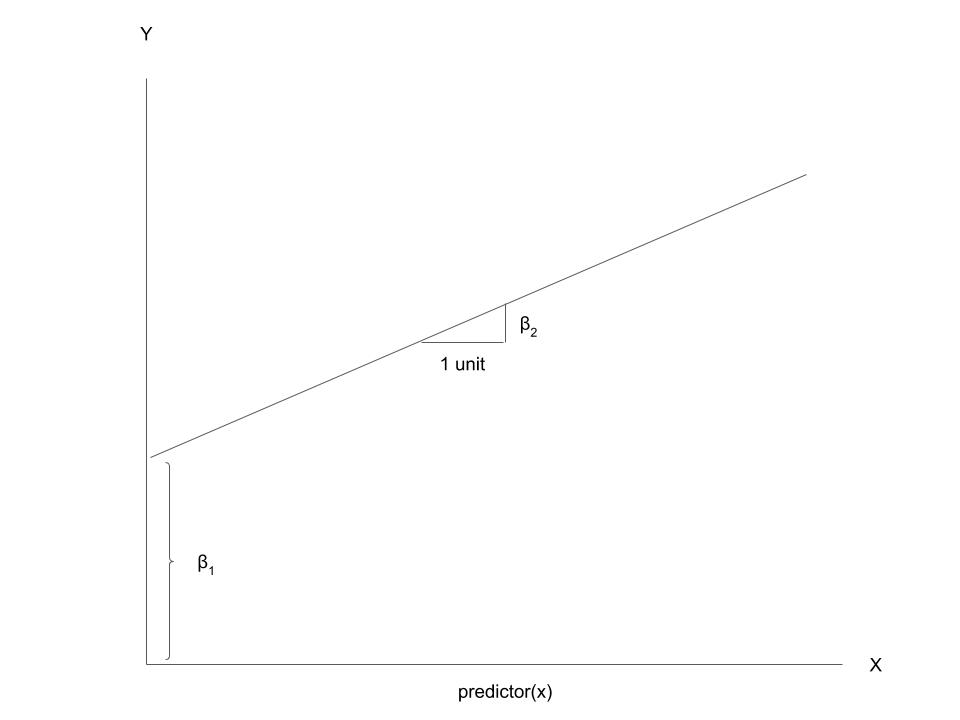
Linear Regression 線性迴歸方程式:\(Y=\beta_{1}+\beta_{2}*X+\varepsilon\)
Example Problem
使用資料集為R dataset套件中的airquality。此資料集主要搜集自1973年5月到9月,每日空氣品質相關的衡量指標,包括臭氧濃度、太陽輻射、平均風速、最高溫度,以及資料月份與資料日。
分析目標:找出影響空氣中臭氧(Ozone)濃度的重要影響因子與關係。
目標變數(依變數):連續變數(臭氧濃度,Ozone)
預測變數(自變數):連續/類別變數(太陽輻射Solar.R、平均風速Wind、最高溫度Temp、資料月份Month、資料日Day)(*此資料集剛好都是連續變數)
為了達成分析目標,主要的資料處理與分析架構會包括以下步驟:
- 資料載入與檢視
- 資料探索(Exploratory Data Analysis, EDA):視覺化分析
- 視覺化預測變數與目標變數間的關係:相關係數矩陣、散佈圖scatter plot
- 偵測離群值:盒須圖box plot
- 檢查預測變數分佈是否為常態分佈(鐘型)而沒有左右偏移:機率密度圖density plot
- 資料前處理
- 離群值處理
- 標準化-使變數間關係衡量不受單位規模數值影響
- 變數轉換-使變數接近常態分佈,以符合模型假設
- 遺失值填補-使用MICE()套件來預測遺失值
- 建立預測線性模型
- Pooling – 綜合多組遺失值填補後的datasets建立回歸模型,並摘要模型配適結果
- CompleteData – 挑選其中一組遺失填補後的dataset建立回歸模型,並摘要模型配適結果
- 線性回歸模型適合度診斷
- 資料是否符合線性迴歸模型假設
- 使用gvlma套件檢測
- 使用shapiro test 來看變數是否成常態分佈
- 模型驗證
- 檢視(比較)模型配適能力常用指標
- 80% 訓練 20%驗證
- 真實值與預測值相關性(Correlation)
- 正確率(min_max_accuracy)
- 錯誤率(MAPE ,Mean absolute percentage error)
- 加強版模型效果驗證:K-fold Cross Validation
- mean squared error
- 結論
1. 資料載入與檢視
載入資料
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 1. Load and View Dataset library(datasets) # 載入今天分析主要會用到的資料集:AirQuality data("airquality") inputData # 查看資料結構:資料變數、型態 str(inputData) # 'data.frame': 153 obs. of 6 variables: # $ Ozone : int 41 36 12 18 NA 28 23 19 8 NA ... # $ Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ... # $ Wind : num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ... # $ Temp : int 67 72 74 62 56 66 65 59 61 69 ... # $ Month : int 5 5 5 5 5 5 5 5 5 5 ... # $ Day : int 1 2 3 4 5 6 7 8 9 10 ... |
檢視資料
|
1 2 3 4 5 6 7 8 9 10 11 |
# 資料欄位詳細說明可在console輸入: ?datasets::airquality # 查看資料頭幾列 head(inputData) head(inputData) # Ozone Solar.R Wind Temp Month Day # 1 41 190 7.4 67 5 1 # 2 36 118 8.0 72 5 2 # 3 12 149 12.6 74 5 3 # 4 18 313 11.5 62 5 4 # 5 NA NA 14.3 56 5 5 # 6 28 NA 14.9 66 5 6 |
2. 資料探索(Exploratory Data Analysis, EDA)
基本敘述統計
使用summary()函數查看基本敘述統計。可以看到此資料集共有153列,以及6個特徵變數的最大最小值、第一與第三分位數以及遺失值數量。
|
1 2 3 4 5 6 7 8 9 10 11 |
# mean,median,25th and 75th quartiles,min,max, NA數量 summary(inputData) # Ozone Solar.R Wind Temp Month Day # Min. : 1.0 Min. : 7 Min. : 1.70 Min. :56.0 Min. :5.00 Min. : 1.0 # 1st Qu.: 18.0 1st Qu.:116 1st Qu.: 7.40 1st Qu.:72.0 1st Qu.:6.00 1st Qu.: 8.0 # Median : 31.5 Median :205 Median : 9.70 Median :79.0 Median :7.00 Median :16.0 # Mean : 42.1 Mean :186 Mean : 9.96 Mean :77.9 Mean :6.99 Mean :15.8 # 3rd Qu.: 63.2 3rd Qu.:259 3rd Qu.:11.50 3rd Qu.:85.0 3rd Qu.:8.00 3rd Qu.:23.0 # Max. :168.0 Max. :334 Max. :20.70 Max. :97.0 Max. :9.00 Max. :31.0 # NA's :37 NA's :7 |
視覺化分析
視覺化預測變數與目標變數間的關係
使用GGally套件中ggcorr()來查看各變數間的相關係數強弱。
|
1 2 3 4 5 |
library("GGally") # ggcorr(): Plot a correlation matrix # The function ggcorr() draws a correlation matrix plot using ggplot2. ggcorr(data = inputData, palette = "RdYlGn", label = TRUE, label_color = "black") |
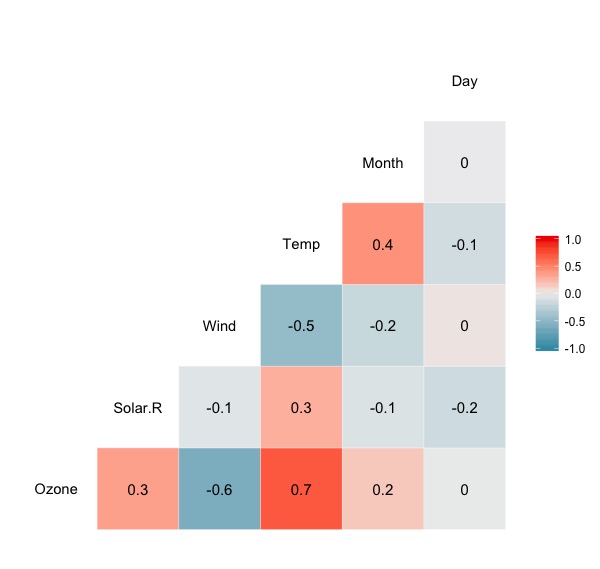
由上圖可以觀察到
(1)具有較強正相關性(相關係數>=0.4)的變數關係有:
- 氣溫(Temp)&月份(Month)
- 臭氧濃度(Ozone)與氣溫(Temp)
(2)具有較強負相關性(相關係數<= -0.4)的變數關係有:
- 風速(Wind)與氣溫(Temp)
- 臭氧濃度(Ozone)與風速(Wind)
但僅參考相關係數,並無法知道兩者是否符合線性關係。
散佈圖scatter plot & 機率密度圖
|
1 2 |
# 使用 ggpairs() 函數產生多個變數間關係的視覺化矩陣散佈圖 ggpairs(data = inputData) |
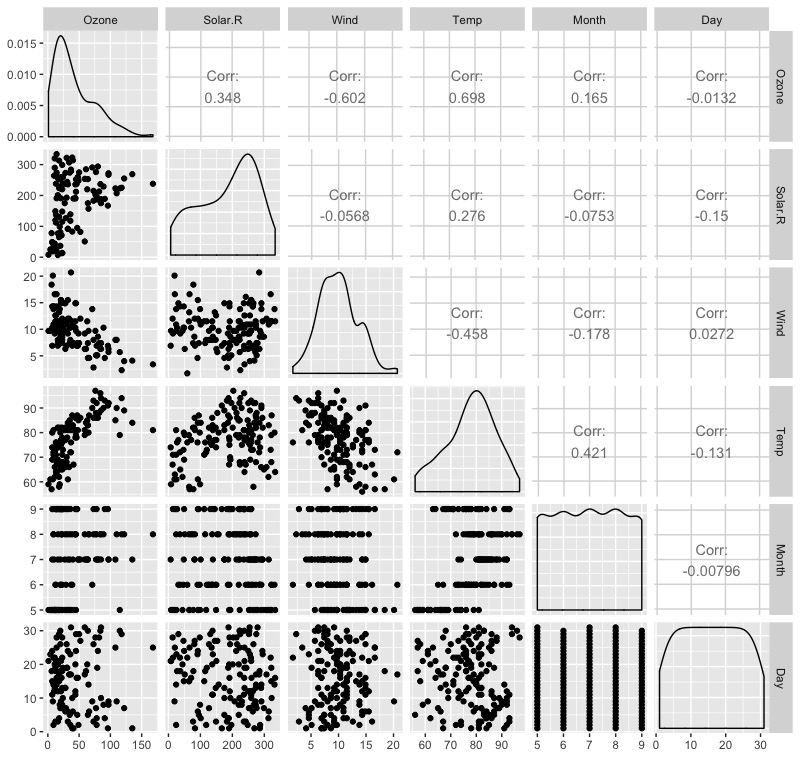
由上圖可以觀察到三種數據型態,分別為:
- 對角線上各個變數的機率密度分佈(用來檢視變數分佈是否為常態)
- 除了Temp稍微看似常態,其餘變數Ozone(右偏嚴重)、Solar.R、Wind都不太滿足常態分佈。
- 左上方三角區塊變數間的相關係數數值大小
- 可以與前面ggcorr()畫的圖做比對
- 左下方三角區塊變數間的散佈圖
- 可以發現此散佈圖在繪製時,已自動使用各變數的最大最小值將數值標準化,所以變數間的散佈圖將不受尺度大小所影響,都剛好在方形的繪圖範圍中。
雖然ggpar可以一次畫出全部,但如果要進一步加上趨勢輔助線,看變數x和y是否為線性關係,可以使用下列語法檢視。
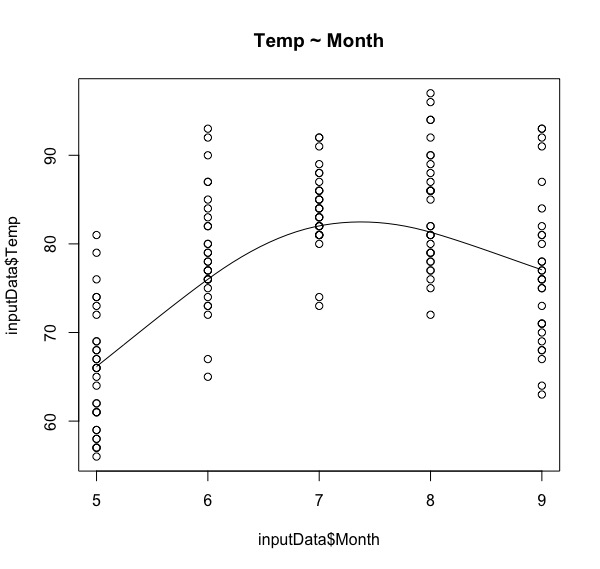
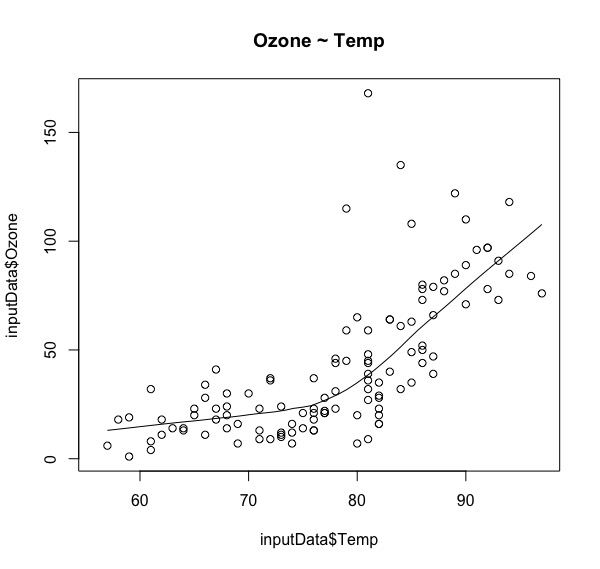
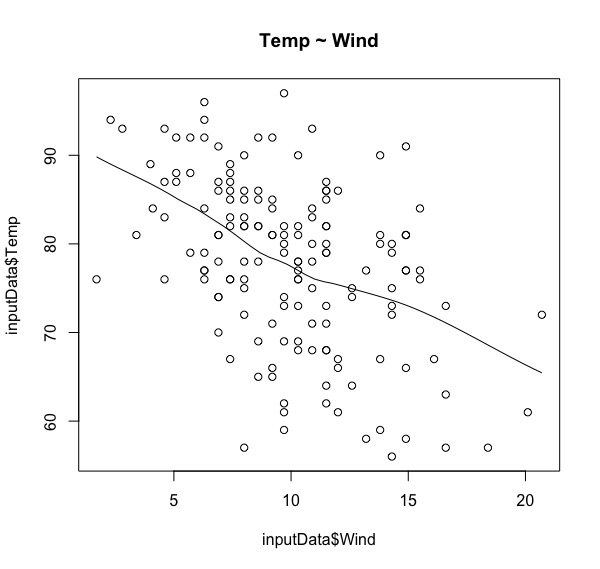
我們將剛剛得知有較強相關性的變數關係畫成散佈圖如下。(Ozone, Temp, Wind, Month)
|
1 2 3 4 |
scatter.smooth(x = inputData$Month, y = inputData$Temp,main = "Temp ~ Month") scatter.smooth(x = inputData$Temp, y = inputData$Ozone,main = "Ozone ~ Temp") scatter.smooth(x = inputData$Wind, y = inputData$Ozone,main = "Ozone ~ Wind") scatter.smooth(x = inputData$Wind, y = inputData$Temp,main = "Temp ~ Wind") |
由上面四張散佈圖,可大略看到線性關係如下:
- 雖然氣溫和部分月份數值成正向關,但根據常識,這並不是我們希望的正向關。
- 臭氧濃度會隨著氣溫上升而上升。
- 臭氧濃度會隨著風速上升而下降。
- 氣溫會隨著風速上升而下降。
離群值偵測
經過上述變數關係探索後,我們將僅針對聚焦後的變數(Ozone,Temp,Wind),進行偵測離群值。
我們將使用合鬚圖(box-plot)法來偵測離群值。
|
1 2 3 |
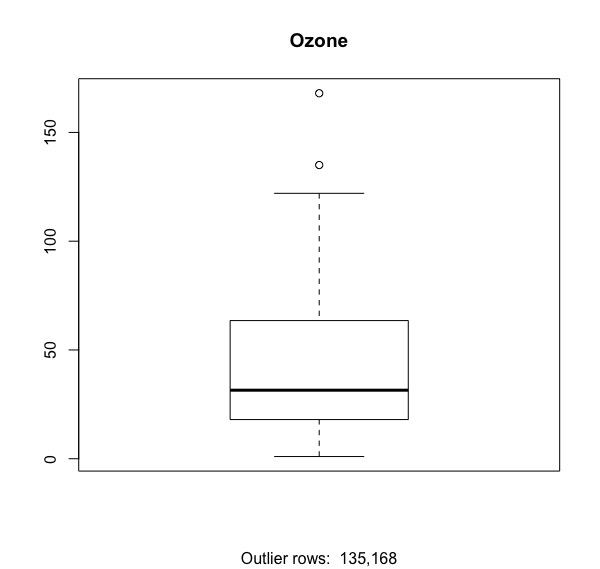
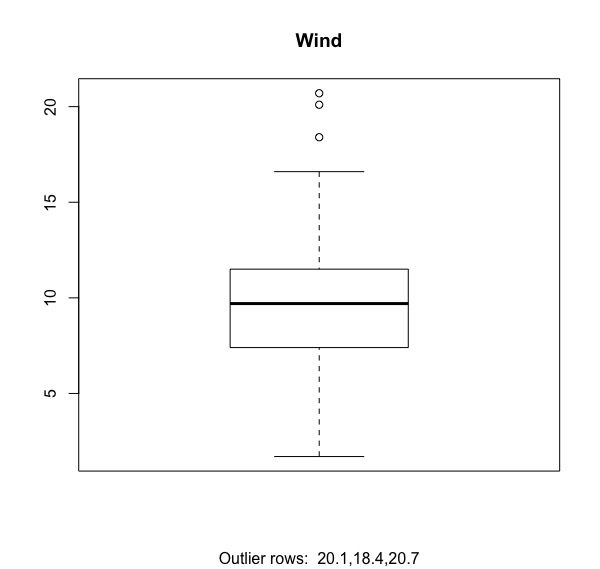
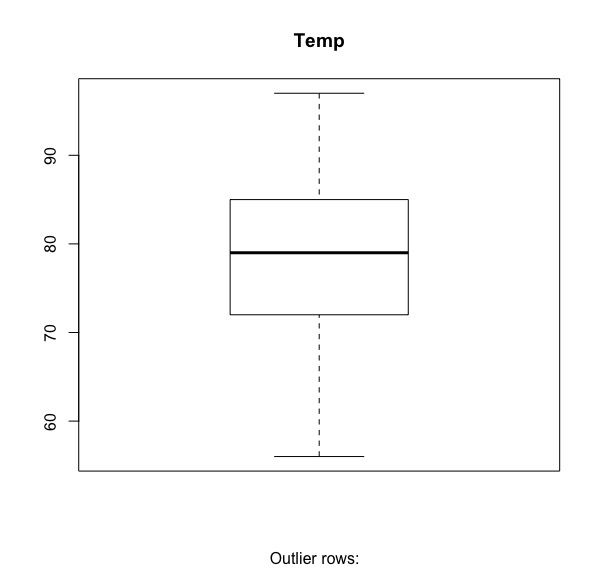
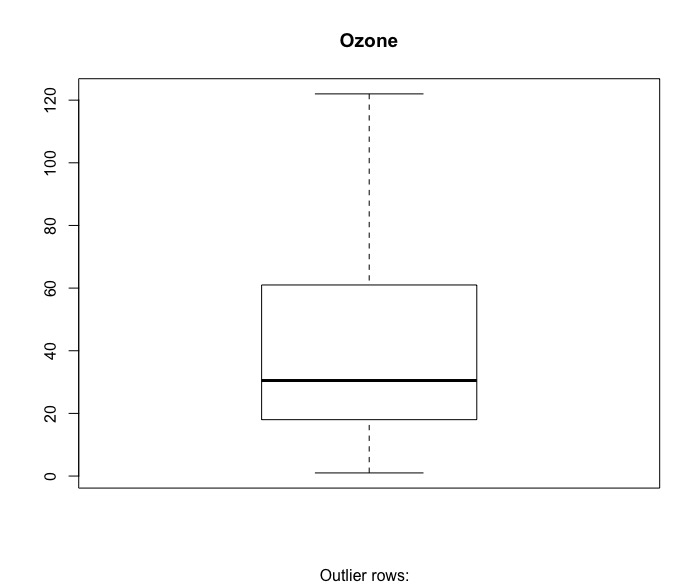
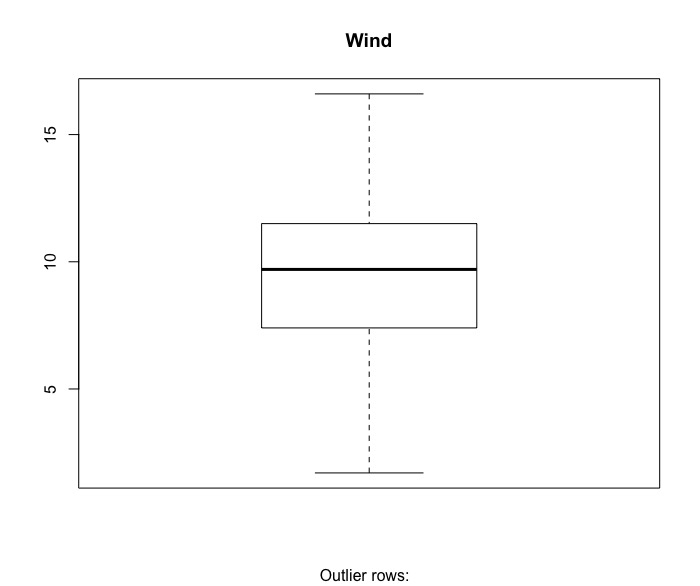
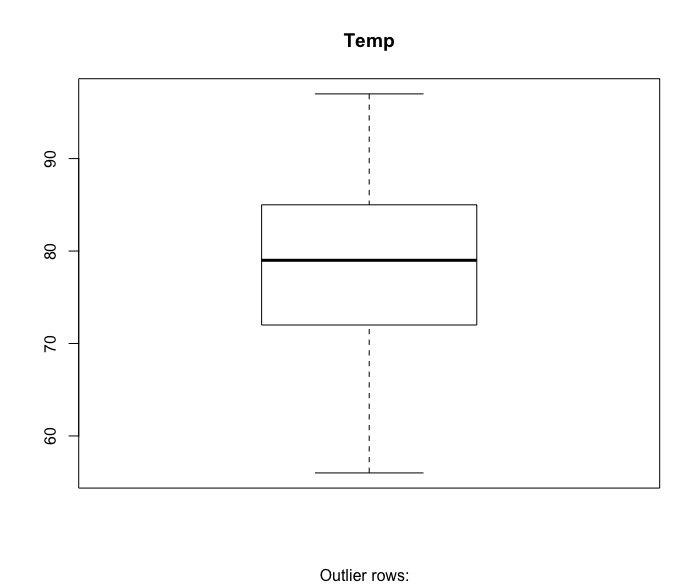
boxplot(inputData$Ozone, main="Ozone", sub=paste("Outlier rows: ", paste(boxplot.stats(inputData$Ozone)$out, collapse = ","))) #有離群值 boxplot(inputData$Wind, main="Wind", sub=paste("Outlier rows: ", paste(boxplot.stats(inputData$Wind)$out, collapse = ","))) #有三個離群值 boxplot(inputData$Temp, main="Temp", sub=paste("Outlier rows: ", paste(boxplot.stats(inputData$Temp)$out, collapse = ","))) #無離群值 |
由盒鬚圖可知,臭氧濃度(Ozone)跟風速(Wind)都有一些離群值。
由上述發現可知,針對聚焦後的變數(Ozone, Temp, Wind),接下來需要處理:
- 離群值處理:Ozone(2), Wind(3)。
- 變數標準化: 使不衡量尺度(單位)間的變數關係不受數值大小所影響。
- 變數轉換:盡可能讓變數分佈符合常態,以符合線性迴歸基本假設。
- 空值填補:Ozone(37)。
3. 資料前處理
3-1. 離群值處理
針對聚焦的三個變數(Ozone,Temp,Wind),本範例會將離群值填補為NA,再之後跟其他空值一併使用MICE方法預測。
偵測離群值(回傳的是離群數值,而非資料列index)。
|
1 2 3 4 5 6 |
boxplot.stats(inputData$Ozone)$out # [1] 135 168 boxplot.stats(inputData$Wind)$out # [1] 20.1 18.4 20.7 boxplot.stats(inputData$Temp)$out # integer(0) |
將離群值填補為NA。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 將遺失值用NA填補 tempData outlier x[x > quantile(x,probs = 0.75,na.rm = T) + 1.5 * IQR(x, na.rm = T) | x x } # apply()的第一個參數只能接受「矩陣」物件,意味著所有元素必須是同一類 # 若用在其他結構的物件,如data.frame,他就會先被轉換成matrix tempData # tempData tempData |
檢視離群值處理後的結果。
|
1 2 3 4 5 6 7 8 9 10 |
summary(tempData) #check Ozone NA數為37+2, Wind NA數為3 # Ozone Solar.R Wind Temp Month Day # Min. : 1.0 Min. : 7 Min. : 1.70 Min. :56.0 Min. :5.00 Min. : 1.0 # 1st Qu.: 18.0 1st Qu.:116 1st Qu.: 7.40 1st Qu.:72.0 1st Qu.:6.00 1st Qu.: 8.0 # Median : 30.5 Median :205 Median : 9.70 Median :79.0 Median :7.00 Median :16.0 # Mean : 40.2 Mean :186 Mean : 9.76 Mean :77.9 Mean :6.99 Mean :15.8 # 3rd Qu.: 60.5 3rd Qu.:259 3rd Qu.:11.50 3rd Qu.:85.0 3rd Qu.:8.00 3rd Qu.:23.0 # Max. :122.0 Max. :334 Max. :16.60 Max. :97.0 Max. :9.00 Max. :31.0 # NA's :39 NA's :7 NA's :3 |
檢視離群值處理後變數分佈的變化。
|
1 2 3 4 5 6 7 |
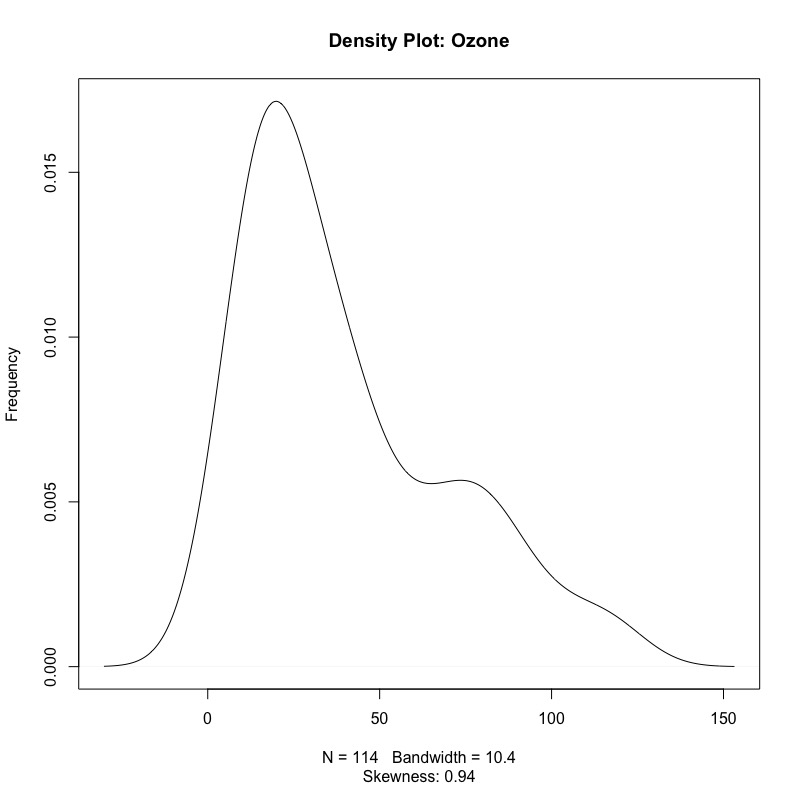
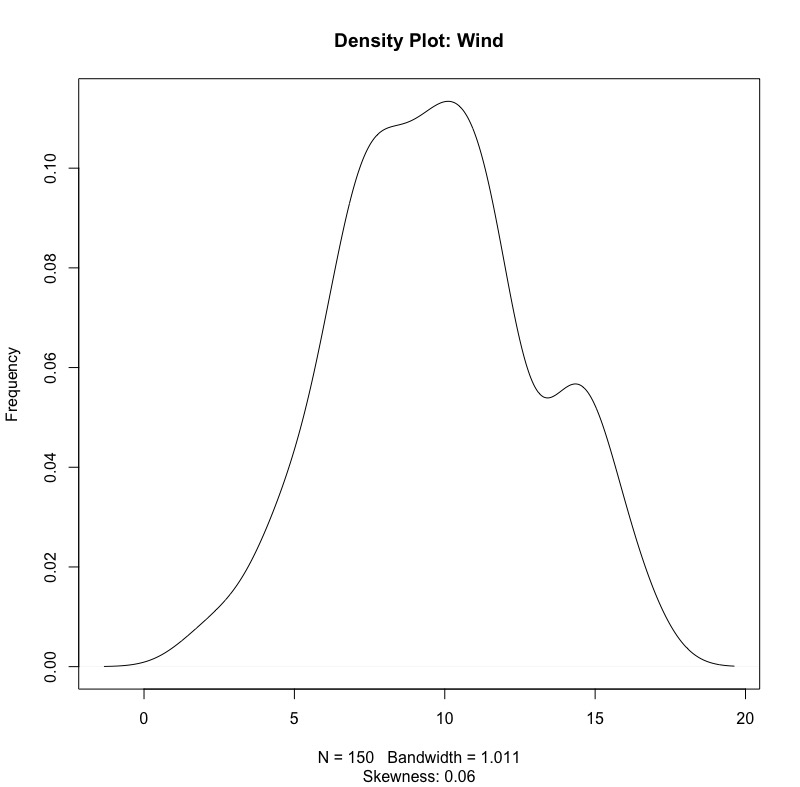
# 經過極端值處理後: # Ozone超級偏(skewness = 1.21 -> 0.94) plot(density(tempData$Ozone, na.rm = TRUE), main="Density Plot: Ozone", ylab="Frequency", sub=paste("Skewness:", round(e1071::skewness(tempData$Ozone, na.rm = TRUE), 2))) # Wind 平均值右偏(skewness = 0.34 -> 0.06) plot(density(tempData$Wind, na.rm = TRUE), main="Density Plot: Wind", ylab="Frequency", sub=paste("Skewness:", round(e1071::skewness(tempData$Wind, na.rm = TRUE), 2))) # Temp 平均值左篇(skewness = -0.37 -> =0.37)沒影響 plot(density(tempData$Temp, na.rm = TRUE), main="Density Plot: Temp", ylab="Frequency", sub=paste("Skewness:", round(e1071::skewness(tempData$Temp, na.rm = TRUE), 2))) |
可以看到:
- Ozone skewness有減少(skewness = 1.21 -> 0.94),但視覺上還是沒有非常接近常態分佈。
- Wind的skewness有從0.34減少到0.06,視覺上已接近常態。
- Temp的部份因為透過box-plot沒有偵測到明顯離群值,故在此沒有變化。
用新的資料偵測離群值,可發現使用box-plot法,已無離群值。
|
1 2 3 4 |
# (2)outlier detection 離群值偵測 =>都沒有了 boxplot(tempData$Ozone, main="Ozone", sub=paste("Outlier rows: ", paste(boxplot.stats(tempData$Ozone)$out, collapse = ","))) #有離群值 boxplot(tempData$Wind, main="Wind", sub=paste("Outlier rows: ", paste(boxplot.stats(tempData$Wind)$out, collapse = ","))) #有三個離群值 boxplot(tempData$Temp, main="Temp", sub=paste("Outlier rows: ", paste(boxplot.stats(tempData$Temp)$out, collapse = ","))) #無黎群值 |
3-2. 標準化
將所有變數標準化(0 to 1)。
|
1 2 |
tempData2 tempData2 |
3-3. 變數轉換(\(X_{transform} = \log_{10}X\))
透過變數log10轉換,來使變數更近似常態分配(僅針對Ozone)。
|
1 2 3 |
subTempData subTempData2 tempData2$Ozone_log10 |
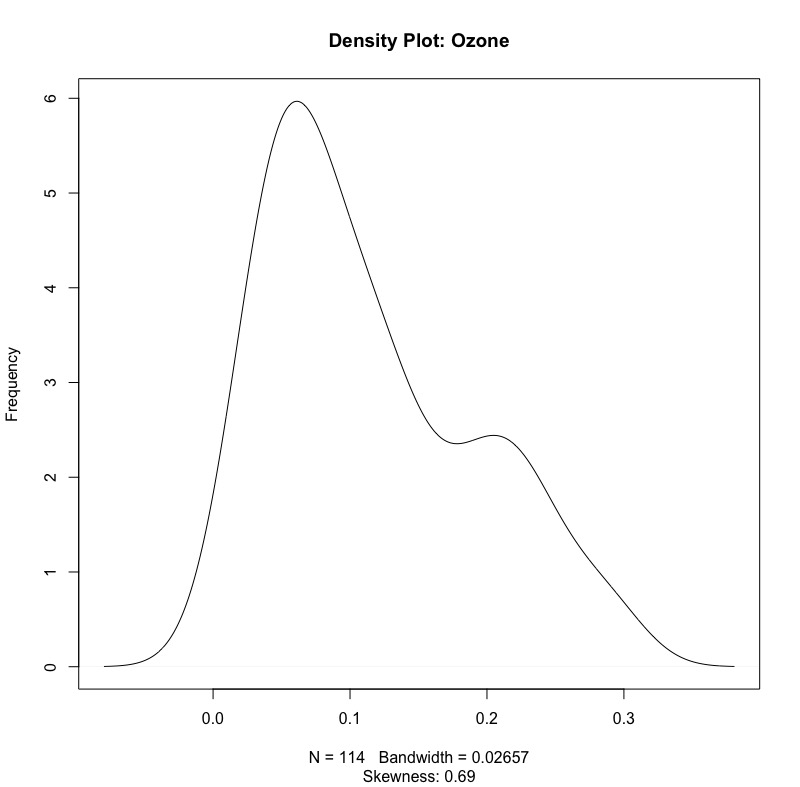
檢視變數轉換後Ozone的機率密度分佈圖。
|
1 2 |
# Ozone_log10(skewness = 1.21 -> 0.94 ->0.69) plot(density(tempData2$Ozone_log10, na.rm = TRUE), main="Density Plot: Ozone", ylab="Frequency", sub=paste("Skewness:", round(e1071::skewness(tempData2$Ozone_log10, na.rm = TRUE), 2))) |
可以發現經log10轉換後的Ozone_log10的skewness有降低,但視覺上分佈還是不是那麼常態。(skewness = 1.21 -> 0.94 ->0.69)
3-4. 空值填補(MICE, Multivariate Imputation by Chained Equations)
當一個特徵變數空值資料占比超過5%就有必要做空值填補之處理。我們建立一個函數用來檢查每個特徵變數遺失資料列佔比。可以發現臭氧Ozone的遺失比例高達25%(原始資料遺失+離群值NA)。
|
1 2 3 4 5 |
pMiss apply(tempData2[,-1],2,pMiss) # Solar.R Wind Temp Month Day Ozone_log10 # 4.575163 1.960784 0.000000 0.000000 0.000000 25.490196 |
在此我們選擇使用MICE Package來處理Ozone的遺失值。(更多有關遺失值處理請參考:「遺失值處理方法」)
MICE代表: Multivariate Imputations by Chained Equations (MICE),具有以下幾個特點:
- 主要可用來產生多元變數(multivariate)的多組空值填補值(multiple imputations)(可透過mice()函式中的參數m,number of mutiple imputations,來指定要產生幾組填補值解,預設為5組)。
- 透過Gibbs sampling法來對多元變數產稱多組空值填補值。
- MICE填補方法是採用Fully Conditional Specification,即每一個不完整的變數都是分別用獨立的模型來預測空值的。
- MICE可處理連續型變數(continuous)、二元變數(binary)、無順序類別型變數(unordered categorical)、有序類別變數(ordered categorical)。
- MICE在預測目標欄位時(target column),預設會使用其他非目標欄位來作為預測變數(predictors)。如遇預測變數本身也不完整的情況,最新產生的一組填補值會被用來完整預測變數,再進行目標變數的填補預測。
- 我們可以替不同欄位指定各自的單變數填補模型(univariate imputation model),使用方法範例:mice(data, meth=c(‘sample’,’pmm’,’logreg’,’norm’)))。
- 單變數填補模型可以使用內建的方法或是自訂方法(mice.impute.myfunc)(mice(method = c(“xxx”, “myfunc“))。
- 常見的幾種內建填補模型包括:
- pmm (Predictive mean matching) : 任何變數型態
- cart (Classification and regression trees) : 任何變數型態
- rf (Random forest imputations) : 任何變數型態
- logreg (Logistic regression) : 二元類別型態 (binary)
MICE package套件中的主要函式說明:
- md.pattern() : inspect the missing data pattern
- mice(): impute the missing values *m* times
- with(): analyzed completed data sets => Performs a computation of each of imputed datasets in data. with (data, expr = formula, …)。將產生的m組填補值套用到計算公式。
- pool(): combine parameter estimates => Pool the results of the repeated analyses。綜合m組填補數據所產生的模型的估計係數(estimates)、標準差(std.error)、和p-value。
- pool.compare() : pool.compare(fit1, fit0, method = c(“wald”, “likelihood”), data = NULL)。使用方法”wald”或”likelihood”來比較兩種模型公式套用在所有填補數據的綜合結果。
- complete(): export imputed data 儲存和輸出其中一組完整填補數據
- ampute(): generate missing data => Generate simulated incomplete data 產生模擬的不完整數據
首先,因為MICE處理遺失值的假設為,資料為隨機遺失(Missing Completely At Random, MCAR),所以在使用套件前,我們先使用mice套件中的md.pattern()函數來檢視資料遺失分佈的狀況。我們可以看到有106列資料是完整的,37列資料缺Ozone,5列資料缺Solar.R,2列資料同時缺Ozone&Solar.R。3列資料缺Wind。Ozone總遺失數為39,Solar.R總遺失數為7,Wind總遺失數為3。
|
1 2 3 4 5 6 7 8 9 10 |
library(mice) md.pattern(tempData2[,-1]) # Temp Month Day Wind Solar.R Ozone_log10 # 106 1 1 1 1 1 1 0 # 37 1 1 1 1 1 0 1 # 5 1 1 1 1 0 1 1 # 2 1 1 1 1 0 0 2 # 3 1 1 1 0 1 1 1 # 0 0 0 3 7 39 49 |
我們使用VIM(Visualization and Imputation of Missing Values)套件中的aggr()函數將上述結果用更有效的視覺化圖表來檢視。
|
1 2 |
library(VIM) aggr_plot |
- 左圖:各特徵變數的遺失資料比例
- 右圖:遺失狀況分佈pattern。由圖可知,有近7成資料是完整的,單單遺失Ozone的資料列高達近25%。
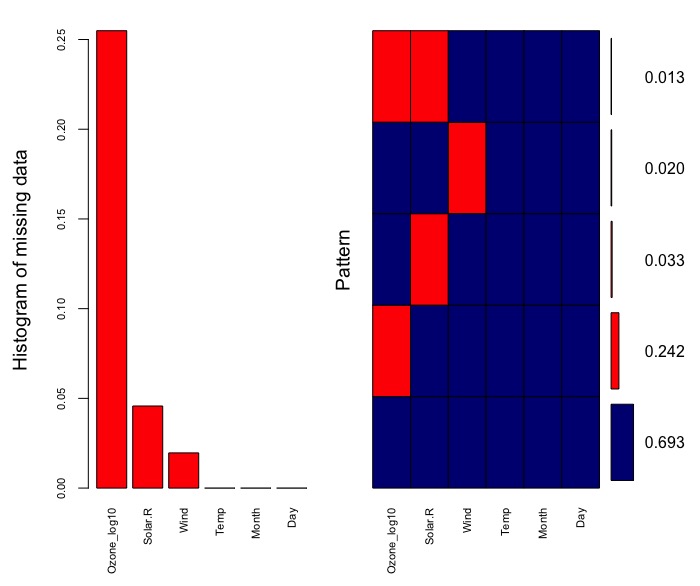
而如何檢視資料的遺失分佈是屬於隨機(Missing Completely At Random, MCAR),就是使用VIM套件的marginplot()函數。關於marginplot()的一些特性如下:
- 一次只能畫出兩維度(變量A&B)遺失分佈關係。在此,因為 Ozone和Solar.R的遺失比例最高,我們將檢視此二變數遺失分佈是否隨機
- 圖的兩軸最外側盒鬚圖:變量A中,對應變量B完整(藍色)/遺失(紅色)的分佈。
- 圖的兩軸內側散佈圖:單一變量A在的變量B發生遺失值的散佈圖。
- 圖的最左下角為變量A與變量B同時遺失的列數。其上方與右方數字則分別表單變量遺失的列數。
- 圖中央則為兩變數A&B的散佈圖。
- 如果IQR區間重疊,且盒鬚圖分佈相似,則變量A與變量B的遺失值分佈為隨機,符合MCAR假設。
|
1 2 |
# Solar.R & Ozone_log10 marginplot(tempData2[c(2,7)]) |
我們從下圖可觀察到:
- 圖左側紅色盒鬚圖為Ozone中Solar.R遺失資料點的分佈,藍色則為其餘Ozone資料點分佈。
- 圖下側紅色盒鬚圖為Solar.R中Ozone遺失資料點的分佈,藍色則為其餘Solar.R資料點分佈。
- 從圖兩側我們可以發現,IQR區間是重疊的,且紅色藍色盒鬚圖分佈相似,因此Var1(Solar.R)與Var2(Ozone)的遺失分佈為隨機的,符合MCAR假設。
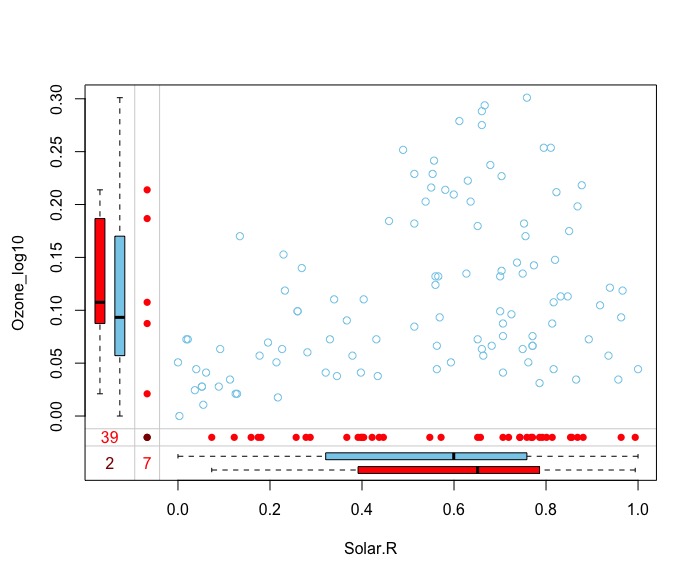
使用mice()函數進行空值填補,幾個重要參數如下:
- 參數m表示要產生幾組填補數據集。預設為產生5組填補數據集。我們將它設為50組。
- 參數method (or meth)表示填補方法。在本範例中,因為變數皆為數值,我將使用預設的pmm(predictive mean matching)法。其他方法包括:
- PMM (Predictive Mean Matching) – For any type variables
- logreg(Logistic Regression) – For binary variables( with 2 levels)
- polyreg(Polytomous logistic regression) – For unordered categorical/factor variables (>= 2 levels)
- polr (Proportional odds model) – For ordered categorical variables ( >= 2 levels)
- 參數maxit表示用於計算遺失值的迭代次數,預設為5。本範例將迭代次數設為50。
|
1 2 3 |
# 先選取後續會分析的變數Wind,Temp,Ozone_log10 tempData2 tempData3 |
使用summary()來看一下填補的結果。可以看到各特徵變數所使用的補值法分別為何,以及填補各目標變數(y)所投入的預測變數(x)。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
summary(tempData3) # Class: mids # Number of multiple imputations: 50 # Imputation methods: # Wind Temp Ozone_log10 # "pmm" "" "pmm" # PredictorMatrix: # Wind Temp Ozone_log10 # Wind 0 1 1 # Temp 1 0 1 # Ozone_log10 1 1 0 |
查看特定特徵值變數填補後的數值可用$imp$var。(列數為該變數有遺失值的列數,行數為各組填補數據集數,本範例為50組)。以Wind為例,遺失的三筆資料,填補後的50組數據集如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#> tempData3$imp$Wind #> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #> 9 0.617 0.846 0.537 0.846 0.577 0.423 0.537 0.349 0.349 0.537 0.349 0.463 0.349 0.349 0.617 0.349 0.812 0.577 0.846 #> 18 0.846 0.577 0.577 0.846 0.537 0.423 0.537 0.577 0.577 0.537 0.886 0.537 0.577 0.537 0.537 0.349 0.846 0.537 0.577 #> 48 0.617 0.617 0.423 0.577 0.886 0.349 0.423 0.926 0.617 0.423 0.537 0.617 0.383 0.423 0.658 0.577 0.383 0.349 0.658 #> 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 #> 9 0.537 0.577 0.537 0.537 1.000 0.846 0.772 0.617 0.658 0.658 0.577 0.846 0.537 0.846 0.423 0.537 0.537 0.423 0.846 #> 18 0.537 0.617 0.537 0.537 0.732 0.423 0.658 0.503 0.423 0.658 0.846 0.577 0.846 0.846 0.537 0.617 0.577 0.423 0.463 #> 48 0.423 0.463 0.309 0.886 0.812 0.195 0.309 0.383 0.383 0.423 0.537 0.658 0.577 0.349 0.309 0.537 0.383 0.537 0.886 #> 39 40 41 42 43 44 45 46 47 48 49 50 #> 9 1.000 1.000 0.846 0.577 0.617 0.537 0.537 0.349 0.503 0.812 0.617 0.537 #> 18 0.577 0.537 0.886 0.732 0.537 0.537 0.537 0.537 0.846 0.846 0.846 0.537 #> 48 0.349 0.309 0.537 0.383 0.658 0.349 0.812 0.886 0.349 0.503 0.383 0.423 |
4. 建立線性模型 linear regression model
最後我們來使用處理好的數據來建立回歸模型。
4-1. Pooling: 使用剛剛填補的50組的資料建模,並摘要綜合50組模型的效果。建模結果顯示預測變數皆為顯著。(p-value < 0.05)
|
1 2 3 4 5 6 7 8 9 |
# 使用不同的datasets(m=50)分別建模,並綜合摘要結果 modelFit1 summary(pool(modelFit1)) # 根據p-value,預測變數Temp & Wind 都有顯著 # estimate std.error statistic df p.value # (Intercept) 0.06810694 0.02245463 3.033091 67.91444 3.255054e-03 # Temp 0.19479181 0.02223289 8.761425 80.70210 2.420286e-13 # Wind -0.10332966 0.02533499 -4.078536 64.42491 1.056795e-04 |
4-2. 使用complete()隨機挑選一組填補後的dataset來建模(預設是第一組,但也可以透過參數調整)。發現模型配適結果也是顯著的(p-value < 0.05)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
completedData modelFit2 summary(modelFit2) # Call: # lm(formula = Ozone_log10 ~ Temp + Wind, data = completedData) # # Residuals: # Min 1Q Median 3Q Max # -0.108651 -0.030307 -0.004117 0.034658 0.142650 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 0.06882 0.01713 4.017 9.29e-05 *** # Temp 0.18569 0.01784 10.409 # Wind -0.10191 0.01883 -5.412 2.42e-07 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.04581 on 150 degrees of freedom # Multiple R-squared: 0.6041, Adjusted R-squared: 0.5988 # F-statistic: 114.4 on 2 and 150 DF, p-value: |
評估係數(Coefficients)指標說明:
- Estimate: 表示各變數的估計係數。
- Std. Error (SE) of Estimate: 估計標準誤,用來衡量估計回歸式的精準度。表示觀測值與回歸線間的分散或離散程度。
\(\beta_{0}, \beta_{1}\)計算方式分別如下:
$$SE(\beta_{0})^2 = \sigma^2[\frac{1}{n}+\frac{\bar{x}^2}{\sum_{i=1}^n (x_{i} – \bar{x})^2}],\space \space SE(\beta_{1})^2 = \frac{\sigma^2}{\sum_{i=1}^n (x_{i} – \bar{x})^2}$$
其中,\(\sigma^2 = Var(\epsilon)\)表示隨機誤差的變異數。
我們可以透過標準誤SE來計算95%信心水準係數區間如下:12345confint(object = modelFit2,level = 0.95)# 2.5 % 97.5 %# (Intercept) 0.03497014 0.10267304# Temp 0.15044504 0.22094442# Wind -0.13912079 -0.06470414
從以上數據來說,在95%信心水準下\(\beta{1}(Temp)\)的係數區間[0.15,0.22]並沒有包括0,也因此我們可以推論說,當溫度升高100度時,log(臭氧濃度)會增加15-22個單位。 - t-value: 衡量\(\beta{1}\)距離0有多少個標準差。t-value越大,p-value越小,表示該變數與目標變數關係顯著。t-value計算公式如下:
$$t = \frac{\beta_{1}-0}{SE(\beta_{1})}$$ - Pr(>|t|): 兩個預測變數p-value都小於0.05(95%信心水準),表示與目標變數有顯著關係。
評估模型正確性(Model Accuracy)指標說明:
我們可以透過以下幾個數值指標來了解模型配適資料的適合度(goodness-of-fit)。
- Residual standard error (RSE):估計誤差標準差(estimate the standard deviation of error \(\epsilon\))。此模型誤差標準差為0.0458 (越小越好),表示平均來說,實際觀測到的臭氧濃度會偏離回歸預測值約0.0458個單位(這是取log轉換後的數值)。
誤差標準差衡量的是平均觀測值偏離回歸的程度。計算公式如下:
$$RSE = \sqrt{\frac{1}{n-2} \sum_{i=1}^n (y_{i} – \hat{y}_{i})^2}$$
RSE除了顯示在sumary(modelFit2)的底端,亦可透過以下sigma()函數取得。12sigma(modelFit2)# [1] 0.04580728
但畢竟RSE評估模型配適資料合適度是用實際觀測值偏離回歸預測值多少個Y單位,無從得知構成模型配適 - R-squared (判定係數): 衡量的是預測變數共解釋了多少變異。\(R^2\)是一個介於0到1的數值,越大越好,且數值不受Y單位所影響。\(R^2\)計算公式如下:
$$R^2 = 1 – \frac{SSR}{SST} = 1 – \frac{\sum_{i=1}^n (y_{i} – \hat{y}_{i})^2}{\sum_{i=1}^n (y_{i} – \bar{y}_{i})^2}$$
除了可以從sumary(modelFit2)最後幾行得知\(R^2\)的資訊,我們亦可透過以下modelr套件中的rsqaure()函數取得。12rsquare(modelFit2, data = completedData)# [1] 0.604058
此模型的預測變數(Temp & Wind)共解釋了60%目標變數(Ozone)的變異。 - Adjusted R-squared: 調整後的\(R^2\)有綜合考量變數總數(模型複雜度)的懲罰效果。此模型adj.\(R^2\)為 0.599(會比\(R^2\)來的小),近似60%。
- F-statistic: F-statistic test是用來檢測是否模型中至少有一預測變數係數不為0(當模型為複回歸時,此檢測結果特別重要)。F統計量的計算公式如下:
$$F = \frac{TSS – RSS/p}{RSS/n-p-1}$$
F統計量越大,p-value越顯著(p<0.05)。
此模型的F統計量為114(越大越好),對應的p-value為 p < 2.2e-16。
5. linear regression 線性回歸模型適合度診斷
5-1. 基本假設檢定
檢視模型配適度一個重要的步驟,就是透過視覺化殘差分佈,來檢視模型基本假設是否皆符合。
|
1 2 3 4 5 6 7 8 9 10 |
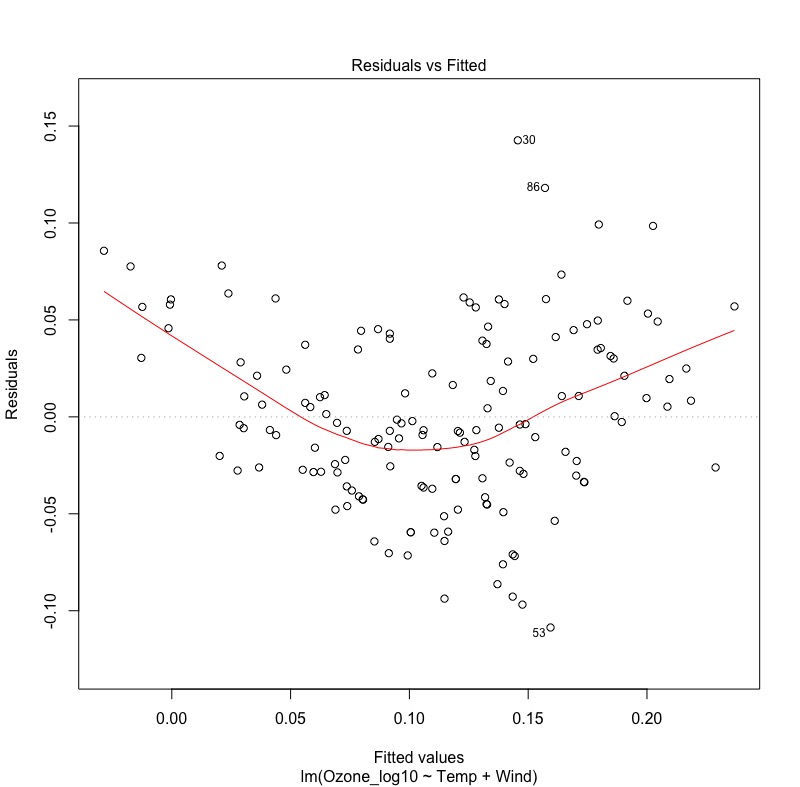
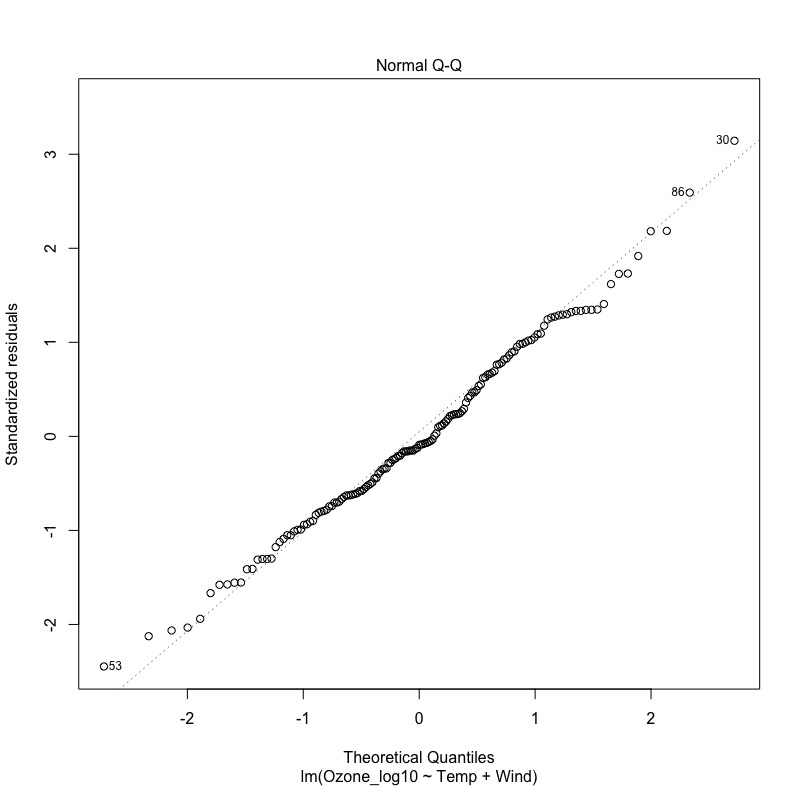
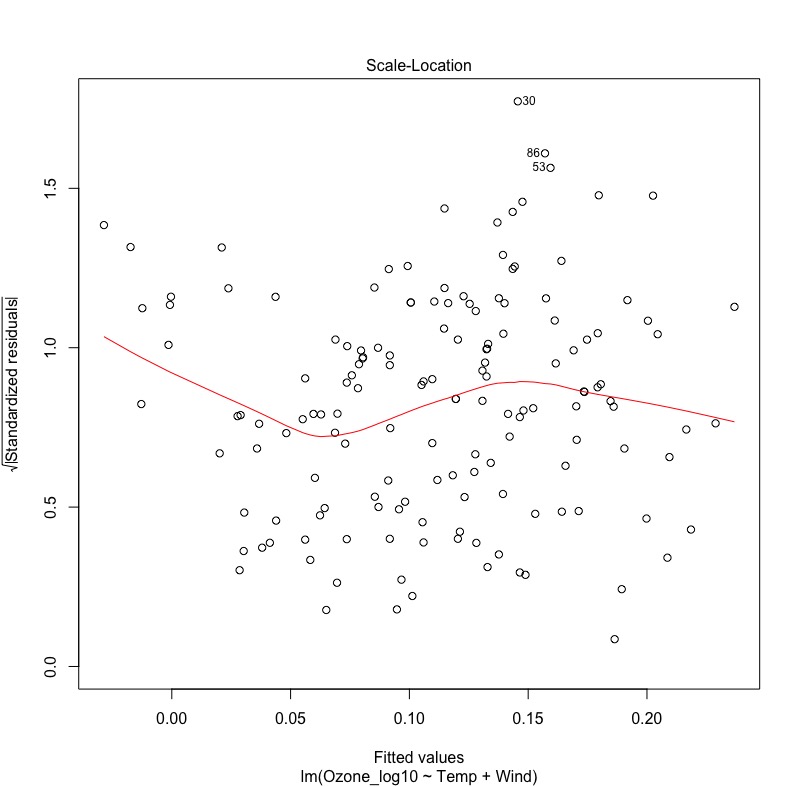
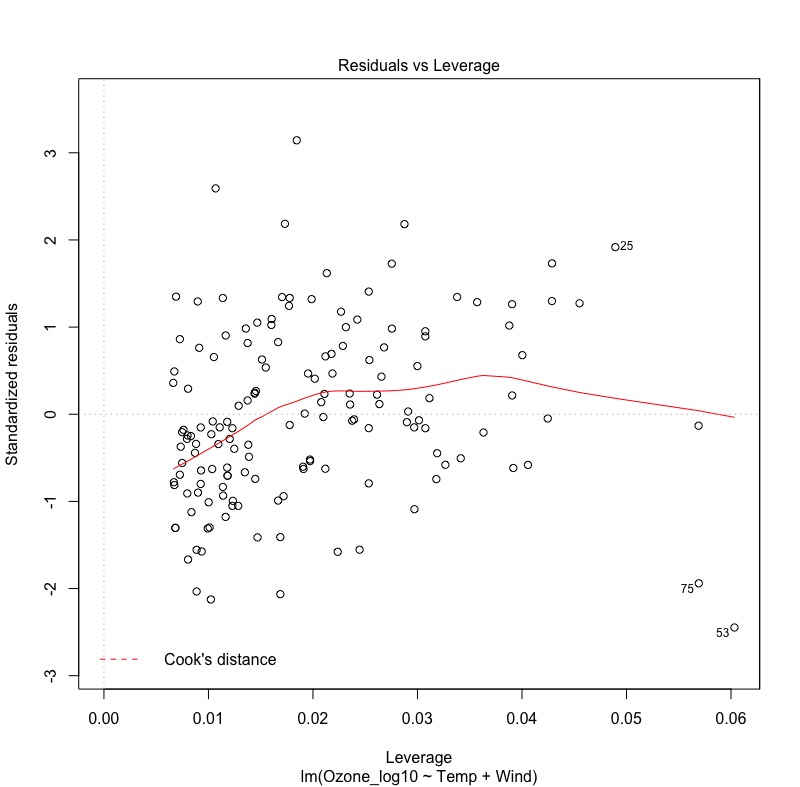
# Reset par to the default values at startup dev.off() # 5.1 是否符合線性迴歸之基本假設:殘差變異數均一性 plot(modelFit2, which = 1) # 殘差變異分佈不在水平線上,且不接近零 # 5.2 殘差是否為常態分佈 plot(modelFit2, which = 2) # 殘差值分佈不在45度線上 # 5.3 標準化殘差分佈亦不成水平線分佈 plot(modelFit2, which = 3) # 5.4 沒有對模型影響力過強的資料點(如果有的話,會出現在虛線cook's distance之外) plot(modelFit2, which = 5) |
由下圖可以發現:
- 左上:殘差變異數不符合均一性。(理想上,希望紅色線條要接近水平線並接近0)
- 右上:殘差分佈不符合常態。(理想上,希望殘差值分佈不在45度線上)
- 左下:標準化殘差變異數不符合均一性。(理想上,希望紅色線條要接近水平線並接近0)
- 右下:檢視是否有對模型影響力過高的資料點。(若是有,資料點將會超過cook’s distance虛線外)
綜合以上,會發現線性模型似乎不適合用來配適此組資料。
5-2. gvlma package
另外,也可以使用gvlma套件來檢定模型是否符合假設。可以發現有部分線性迴歸模型的基礎假設是不成立的。(不過要注意的是,gvlma套件結果相關說明的資料不是很充足。)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
# Check Assumptions Automatically library(gvlma) # mod gvlma(modelFit2) summary(gvlma(modelFit2)) # 但網路上相關資源目前並沒有太多有關gvlma套件產生結果的說明 # Call: # lm(formula = Ozone_log10 ~ Temp + Wind, data = completedData) # # Residuals: # Min 1Q Median 3Q Max # -0.108651 -0.030307 -0.004117 0.034658 0.142650 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 0.06882 0.01713 4.017 9.29e-05 *** # Temp 0.18569 0.01784 10.409 # Wind -0.10191 0.01883 -5.412 2.42e-07 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.04581 on 150 degrees of freedom # Multiple R-squared: 0.6041, Adjusted R-squared: 0.5988 # F-statistic: 114.4 on 2 and 150 DF, p-value: # # # ASSESSMENT OF THE LINEAR MODEL ASSUMPTIONS # USING THE GLOBAL TEST ON 4 DEGREES-OF-FREEDOM: # Level of Significance = 0.05 # # Call: # gvlma(x = modelFit2) # # Value p-value Decision # Global Stat 31.296325 2.664e-06 Assumptions NOT satisfied! # Skewness 1.321357 2.503e-01 Assumptions acceptable. # Kurtosis 0.004069 9.491e-01 Assumptions acceptable. # Link Function 28.858171 7.788e-08 Assumptions NOT satisfied! # Heteroscedasticity 1.112728 2.915e-01 Assumptions acceptable. |
5-3. shapiro test常態分佈檢定
另外,我們亦使用shapiro test 來看鎖定變數是否成常態分佈(H0: 分佈等於常態分佈)。可以發現除了Wind符合常態分配,另外兩個變數都離常態分佈有些距離。因此除非進一步將變數有效轉換以符合常態,否則不適合用線性迴規模性來進行資料配適。
|
1 2 3 4 5 |
options(scipen = 999) normality_test normality_test # Wind Temp Ozone_log10 # 0.0928 0.0093 0.0000 |
6. 模型驗證Validation
6-1. 常見模型效果評估指標
| STATISTIC | CRITERION |
| R-Squared | Higher the better (> 0.70)。表示解釋變異量佔總變異量的百分比。 |
| Adj R-Squared | Higher the better。表示調整後(對模型複雜度加入懲罰)解釋變異量佔總變異量的百分比。 |
| F-Statistic | Higher the better。 |
| Std. Error (標準誤) | Closer to zero the better。 (表抽樣結果與母體的偏差) |
| t-statistic | Should be greater 1.96 for p-value to be less than 0.05 |
| AIC | Lower the better |
| BIC | Lower the better |
| Mallows cp | Should be close to the number of predictors in model |
| MAPE (Mean absolute percentage error) | Lower the better |
| MSE (Mean squared error) | Lower the better |
| Min_Max Accuracy => mean(min(actual, predicted)/ max(actual, predicted)) |
Higher the better |
6-2. 模型驗證(80%Training20%Testing)
將資料隨機區分為訓練資料集(80%)與測試資料集(20%)
|
1 2 3 4 5 |
# 將資料切分為訓練集與測試集 set.seed(1234) trainingRowIndex trainingData testData |
使用訓練及資料建置模型 & 使用測試集資料預測結果。並摘要訓練的模型效果summary(mod)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 使用訓練及資料建置模型 & 使用測試集資料預測結果 mod predictY summary(mod) # Call: # lm(formula = Ozone_log10 ~ ., data = trainingData, na.action = na.omit) # # Residuals: # Min 1Q Median 3Q Max # -0.099618 -0.031069 -0.003893 0.032104 0.138297 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 0.08839 0.02154 4.103 0.0000812697310 *** # Wind -0.11489 0.02344 -4.901 0.0000035281189 *** # Temp 0.16479 0.02187 7.534 0.0000000000188 *** # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 0.04639 on 104 degrees of freedom # Multiple R-squared: 0.5734, Adjusted R-squared: 0.5652 # F-statistic: 69.89 on 2 and 104 DF, p-value: |
檢視模型預測的效果。
|
1 |
actuals_predicts |
計算真實數據與預測數據的相關係數:越高越好。
|
1 2 |
cor(actuals_predicts,use="complete.obs") # 0.8136252 cor(actuals_predicts,use="pairwise.complete.obs") # 0.8136252 |
計算AIC, BIC => 越低越好。
|
1 2 3 4 |
AIC(mod) # [1] -348.5126 BIC(mod) # [1] -337.8213 |
計算模型預測正確率min_max_accuracy: 70.4% = > 越高越好。
|
1 2 3 |
min_max_accuracy min_max_accuracy # [1] 0.7036471 |
計算模型預測錯誤率 MAPE (Mean absolute percentage error): 56% => 越低越好。
|
1 2 3 |
mape mape # [1] 0.5598302 |
6-3. 加強版模型驗證: K-fold Cross Validation
使用k-fold交叉驗證。
|
1 2 |
library(DAAG) cvResults |
查看交叉驗證的平均平方誤差(MSE):越低越好。
|
1 2 3 |
# MSE (Mean squared error): Lower the better attr(cvResults, 'ms') # [1] 0.0105 |
交叉5次模型配適結果圖如下。小圖示為模型預測值,大圖示則為真實資料值。可以發現第五次模型擬和的結果與其他四次有較大差異。
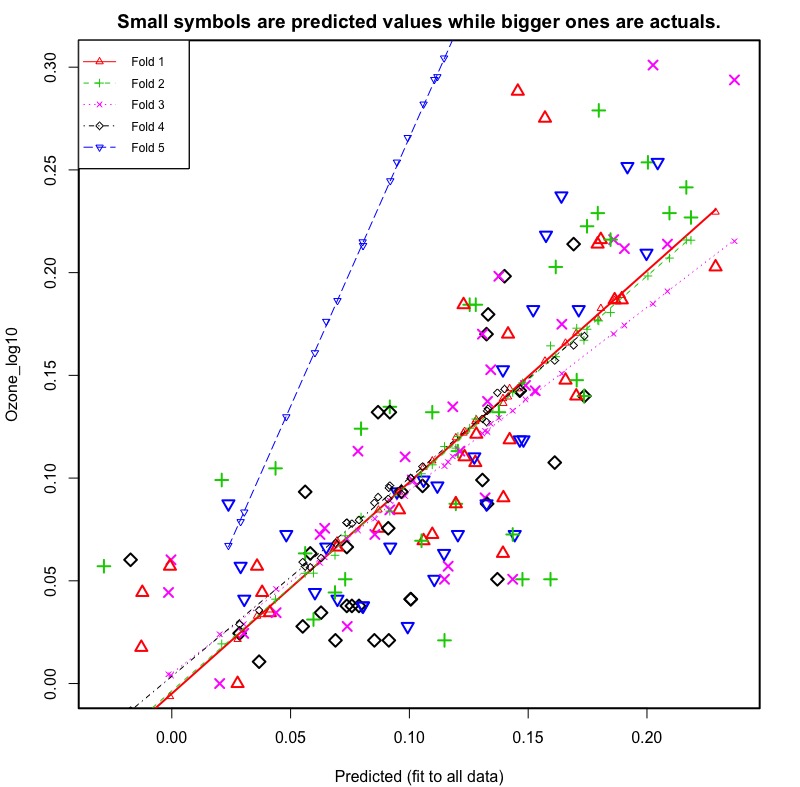
7. 結論
我們可以發現,由於airquality資料型態不接近理想的常態分佈,故使用Linear Regression 線性迴歸模型做資料配適不是很合適(根據「回歸模型適合度診斷」)。如果遇到資料分配非常態時,建議可以考慮其他模型如決策樹(不受限母體分配)。
更多線性回歸模型應用:
更多統計模型學習筆記連結:
- Regularized Regression | 正規化迴歸 – Ridge, Lasso, Elastic Net | R語言
- Logistic Regression 羅吉斯迴歸 | part1 – 資料探勘與處理 | 統計 R語言
- Logistic Regression 羅吉斯迴歸 | part2 – 模型建置、診斷與比較 | R語言
- Decision Tree 決策樹 | CART, Conditional Inference Tree, Random Forest
- Regression Tree | 迴歸樹, Bagging, Bootstrap Aggregation | R語言
- Random Forests 隨機森林 | randomForest, ranger, h2o | R語言
- Gradient Boosting Machines GBM | gbm, xgboost, h2o | R語言
- Hierarchical Clustering 階層式分群 | Clustering 資料分群 | R統計
- Partitional Clustering | 切割式分群 | Kmeans, Kmedoid | Clustering 資料分群
- Principal Components Analysis (PCA) | 主成份分析 | R 統計
參考文章連結: