Logistic Regression 羅吉斯迴歸 | part2 - 模型建置、診斷與比較

Logistic Regression, 羅吉斯回歸模型，適用於預測二元類別目標變數的發生機率(p)，和線性回歸模型類似，與線性回歸主要不同之處在於：(1) 目標變數是目標事件發生機率P經過log函數轉換成log odds值才進行線性預測，且(2)羅吉斯回歸的各項參數是透過最大概似法(MLE)進行估計的。

Logistic Regression part1 前情提要

「Logistic Regression – part1 – 資料探勘與處理」篇的重點回顧：

探索預測變數自身分佈情況以及各預測變數與目標變數之間的關係。
資料預處理，將類別水準直過多的變數進行簡化。
隨機產生訓練與測試資料集。
計算各預測變數的Information Value來初步判斷各預測變數對目標變數的影響程度。
依據IV值初步從13個變數篩選出6個變數包括：RELATIONSHIP, MARITALSTATUS, AGE, EDUCATIONNUM, CAPITALGAIN,OCCUPATION_rep。

分析資料與問題

Problem: 預測薪資大於50K(ABOVE50K)的影響特徵因素有哪些？

Data: adult dataset (snapshot)

目標變數(1)：ABOVE50K

預測變數(13)：AGE, WORKCLASS, EDUCATION, EDUCATIONNUM, MARITALSTATUS, OCCUPATION, RELATIONSHIP, RACE, SEX, CAPITALGAIN, CAPITALLOSS, HOURSPERWEEK, NATIVECOUNTRY

分析步驟

(part 2 篇會說明步驟6~8的部分)(步驟1~5請參考「Logistic Regression – part1 – 資料探勘與處理」)

資料載入與檢視
資料探勘
資料前處理
產生訓練資料集與測試資料集
計算特徵變數IV值(Information Value)，篩選變數
訓練模型與預測
模型診斷與調整
模型比較(v.s. Machine Learning Methods)

6. 訓練模型與預測

接續「Logistic Regression – part1 – 資料探勘與處理」，我們將近一步針對初步篩選出的6預測變數進行羅基斯回歸模型分析。

logitMod <- glm(formula = ABOVE50K_y ~ RELATIONSHIP + MARITALSTATUS + AGE + EDUCATIONNUM + CAPITALGAIN + OCCUPATION_rep,
                data = trainingData,family = binomial(link = "logit"))
summary(logitMod)

# Call:
#   glm(formula = ABOVE50K_y ~ RELATIONSHIP + MARITALSTATUS + AGE + 
#         EDUCATIONNUM + CAPITALGAIN + OCCUPATION_rep, family = binomial(link = "logit"), 
#       data = trainingData)
# 
# Deviance Residuals: 
#   Min       1Q   Median       3Q      Max  
# -5.2263  -0.5640  -0.2258  -0.0528   3.8139  
# 
# Coefficients:
#   Estimate Std. Error z value             Pr(>|z|)    
# (Intercept)                         -6.2679390  0.3703477 -16.924 < 0.0000000000000002 ***
#   RELATIONSHIP Not-in-family          -0.2201571  0.3288849  -0.669             0.503237    
# RELATIONSHIP Other-relative         -1.5525876  0.3172511  -4.894     0.00000098869035 ***
#   RELATIONSHIP Own-child              -1.6632915  0.3252302  -5.114     0.00000031507745 ***
#   RELATIONSHIP Unmarried              -0.6486702  0.3428225  -1.892             0.058472 .  
# RELATIONSHIP Wife                   -0.0196633  0.0760145  -0.259             0.795884    
# MARITALSTATUS Married-AF-spouse      2.4570045  0.6658794   3.690             0.000224 ***
#   MARITALSTATUS Married-civ-spouse     1.9165557  0.3331962   5.752     0.00000000881763 ***
#   MARITALSTATUS Married-spouse-absent -0.0649140  0.2672163  -0.243             0.808062    
# MARITALSTATUS Never-married         -0.3668251  0.1008955  -3.636             0.000277 ***
#   MARITALSTATUS Separated             -0.1122524  0.1867781  -0.601             0.547845    
# MARITALSTATUS Widowed               -0.1851853  0.1746133  -1.061             0.288897    
# AGE                                  0.0217164  0.0017943  12.103 < 0.0000000000000002 ***
#   EDUCATIONNUM                         0.3058023  0.0103400  29.575 < 0.0000000000000002 ***
#   CAPITALGAIN                          0.0003108  0.0000118  26.331 < 0.0000000000000002 ***
#   OCCUPATION_repBlue-Collar           -0.4800489  0.0701546  -6.843     0.00000000000777 ***
#   OCCUPATION_repOther/Unknown         -1.3267766  0.1312315 -10.110 < 0.0000000000000002 ***
#   OCCUPATION_repProfessional           0.1688849  0.0799712   2.112             0.034702 *  
#   OCCUPATION_repService               -0.4061912  0.0845737  -4.803     0.00000156457927 ***
#   OCCUPATION_repWhite-Collar           0.2455151  0.0699361   3.511             0.000447 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# (Dispersion parameter for binomial family taken to be 1)
# 
# Null deviance: 25162  on 22791  degrees of freedom
# Residual deviance: 15492  on 22772  degrees of freedom
# AIC: 15532
# 
# Number of Fisher Scoring iterations: 7

logitMod

data = trainingData,family = binomial(link = "logit"))

summary(logitMod)

# Call:

# glm(formula = ABOVE50K_y ~ RELATIONSHIP + MARITALSTATUS + AGE +

# EDUCATIONNUM + CAPITALGAIN + OCCUPATION_rep, family = binomial(link = "logit"),

# data = trainingData)

# Deviance Residuals:

# Min 1Q Median 3Q Max

# -5.2263 -0.5640 -0.2258 -0.0528 3.8139

# Coefficients:

# Estimate Std. Error z value Pr(>|z|)

# (Intercept) -6.2679390 0.3703477 -16.924

# RELATIONSHIP Not-in-family -0.2201571 0.3288849 -0.669 0.503237

# RELATIONSHIP Other-relative -1.5525876 0.3172511 -4.894 0.00000098869035 ***

# RELATIONSHIP Own-child -1.6632915 0.3252302 -5.114 0.00000031507745 ***

# RELATIONSHIP Unmarried -0.6486702 0.3428225 -1.892 0.058472 .

# RELATIONSHIP Wife -0.0196633 0.0760145 -0.259 0.795884

# MARITALSTATUS Married-AF-spouse 2.4570045 0.6658794 3.690 0.000224 ***

# MARITALSTATUS Married-civ-spouse 1.9165557 0.3331962 5.752 0.00000000881763 ***

# MARITALSTATUS Married-spouse-absent -0.0649140 0.2672163 -0.243 0.808062

# MARITALSTATUS Never-married -0.3668251 0.1008955 -3.636 0.000277 ***

# MARITALSTATUS Separated -0.1122524 0.1867781 -0.601 0.547845

# MARITALSTATUS Widowed -0.1851853 0.1746133 -1.061 0.288897

# AGE 0.0217164 0.0017943 12.103

# EDUCATIONNUM 0.3058023 0.0103400 29.575

# CAPITALGAIN 0.0003108 0.0000118 26.331

# OCCUPATION_repBlue-Collar -0.4800489 0.0701546 -6.843 0.00000000000777 ***

# OCCUPATION_repOther/Unknown -1.3267766 0.1312315 -10.110

# OCCUPATION_repProfessional 0.1688849 0.0799712 2.112 0.034702 *

# OCCUPATION_repService -0.4061912 0.0845737 -4.803 0.00000156457927 ***

# OCCUPATION_repWhite-Collar 0.2455151 0.0699361 3.511 0.000447 ***

# ---

# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# (Dispersion parameter for binomial family taken to be 1)

# Null deviance: 25162 on 22791 degrees of freedom

# Residual deviance: 15492 on 22772 degrees of freedom

# AIC: 15532

# Number of Fisher Scoring iterations: 7

除了摘要模型，我們另外針對共線性進行檢查。發現變數RELATIONSHIP和MARITALSTATUS有共線性。

# 模型共線性檢查VIF(希望VIF值都在4以下)
library(car)
vif(logitMod)

#                     GVIF Df GVIF^(1/(2*Df))
# RELATIONSHIP   55.704490  5        1.494820
# MARITALSTATUS  56.687207  6        1.399986
# AGE             1.177411  1        1.085086
# EDUCATIONNUM    1.384560  1        1.176673
# CAPITALGAIN     1.018983  1        1.009447
# OCCUPATION_rep  1.531311  5        1.043533

# 模型共線性檢查VIF(希望VIF值都在4以下)

library(car)

vif(logitMod)

# GVIF Df GVIF^(1/(2*Df))

# RELATIONSHIP 55.704490 5 1.494820

# MARITALSTATUS 56.687207 6 1.399986

# AGE 1.177411 1 1.085086

# EDUCATIONNUM 1.384560 1 1.176673

# CAPITALGAIN 1.018983 1 1.009447

# OCCUPATION_rep 1.531311 5 1.043533

因此，我們根據RELATIONSHIP和MARITALSTATUS的IV值，捨棄其中較低者，重新再進行一次模型建置。

logitMod <- glm(formula = ABOVE50K_y ~ RELATIONSHIP + AGE + EDUCATIONNUM + CAPITALGAIN + OCCUPATION_rep,
                data = trainingData,family = binomial(link = "logit"))

summary(logitMod)

# Call:
#   glm(formula = ABOVE50K_y ~ RELATIONSHIP + AGE + EDUCATIONNUM + 
#         CAPITALGAIN + OCCUPATION_rep, family = binomial(link = "logit"), 
#       data = trainingData)
# 
# Deviance Residuals: 
#   Min       1Q   Median       3Q      Max  
# -5.2305  -0.5663  -0.2319  -0.0590   3.5991  
# 
# Coefficients:
#   Estimate  Std. Error z value
# (Intercept)                 -4.39303806  0.15173422 -28.952
# RELATIONSHIP Not-in-family  -2.34469608  0.05835820 -40.178
# RELATIONSHIP Other-relative -3.02210032  0.26185701 -11.541
# RELATIONSHIP Own-child      -3.72243110  0.16395790 -22.704
# RELATIONSHIP Unmarried      -2.66495726  0.09783246 -27.240
# RELATIONSHIP Wife           -0.00985696  0.07585158  -0.130
# AGE                          0.02285379  0.00171654  13.314
# EDUCATIONNUM                 0.30497481  0.01032637  29.534
# CAPITALGAIN                  0.00031083  0.00001181  26.312
# OCCUPATION_repBlue-Collar   -0.47777138  0.07013154  -6.813
# OCCUPATION_repOther/Unknown -1.33506791  0.13132122 -10.166
# OCCUPATION_repProfessional   0.16489267  0.07982984   2.066
# OCCUPATION_repService       -0.40645290  0.08448125  -4.811
# OCCUPATION_repWhite-Collar   0.24924877  0.06989076   3.566
# Pr(>|z|)    
# (Intercept)                 < 0.0000000000000002 ***
#   RELATIONSHIP Not-in-family  < 0.0000000000000002 ***
#   RELATIONSHIP Other-relative < 0.0000000000000002 ***
#   RELATIONSHIP Own-child      < 0.0000000000000002 ***
#   RELATIONSHIP Unmarried      < 0.0000000000000002 ***
#   RELATIONSHIP Wife                       0.896606    
# AGE                         < 0.0000000000000002 ***
#   EDUCATIONNUM                < 0.0000000000000002 ***
#   CAPITALGAIN                 < 0.0000000000000002 ***
#   OCCUPATION_repBlue-Collar       0.00000000000959 ***
#   OCCUPATION_repOther/Unknown < 0.0000000000000002 ***
#   OCCUPATION_repProfessional              0.038871 *  
#   OCCUPATION_repService           0.00000150055853 ***
#   OCCUPATION_repWhite-Collar              0.000362 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# (Dispersion parameter for binomial family taken to be 1)
# 
# Null deviance: 25162  on 22791  degrees of freedom
# Residual deviance: 15542  on 22778  degrees of freedom
# AIC: 15570
# 
# Number of Fisher Scoring iterations: 7

logitMod

data = trainingData,family = binomial(link = "logit"))

summary(logitMod)

# Call:

# glm(formula = ABOVE50K_y ~ RELATIONSHIP + AGE + EDUCATIONNUM +

# CAPITALGAIN + OCCUPATION_rep, family = binomial(link = "logit"),

# data = trainingData)

# Deviance Residuals:

# Min 1Q Median 3Q Max

# -5.2305 -0.5663 -0.2319 -0.0590 3.5991

# Coefficients:

# Estimate Std. Error z value

# (Intercept) -4.39303806 0.15173422 -28.952

# RELATIONSHIP Not-in-family -2.34469608 0.05835820 -40.178

# RELATIONSHIP Other-relative -3.02210032 0.26185701 -11.541

# RELATIONSHIP Own-child -3.72243110 0.16395790 -22.704

# RELATIONSHIP Unmarried -2.66495726 0.09783246 -27.240

# RELATIONSHIP Wife -0.00985696 0.07585158 -0.130

# AGE 0.02285379 0.00171654 13.314

# EDUCATIONNUM 0.30497481 0.01032637 29.534

# CAPITALGAIN 0.00031083 0.00001181 26.312

# OCCUPATION_repBlue-Collar -0.47777138 0.07013154 -6.813

# OCCUPATION_repOther/Unknown -1.33506791 0.13132122 -10.166

# OCCUPATION_repProfessional 0.16489267 0.07982984 2.066

# OCCUPATION_repService -0.40645290 0.08448125 -4.811

# OCCUPATION_repWhite-Collar 0.24924877 0.06989076 3.566

# Pr(>|z|)

# (Intercept)

# RELATIONSHIP Not-in-family

# RELATIONSHIP Other-relative

# RELATIONSHIP Own-child

# RELATIONSHIP Unmarried

# RELATIONSHIP Wife 0.896606

# AGE

# EDUCATIONNUM

# CAPITALGAIN

# OCCUPATION_repBlue-Collar 0.00000000000959 ***

# OCCUPATION_repOther/Unknown

# OCCUPATION_repProfessional 0.038871 *

# OCCUPATION_repService 0.00000150055853 ***

# OCCUPATION_repWhite-Collar 0.000362 ***

# ---

# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# (Dispersion parameter for binomial family taken to be 1)

# Null deviance: 25162 on 22791 degrees of freedom

# Residual deviance: 15542 on 22778 degrees of freedom

# AIC: 15570

# Number of Fisher Scoring iterations: 7

並在重新檢視共線性。可以發現去除MARITALSTATUS後，所有變數的VIF值都小於4了。

library(car)
vif(logitMod)

#                     GVIF Df GVIF^(1/(2*Df))
# RELATIONSHIP   1.197104  5        1.018153
# AGE            1.089616  1        1.043847
# EDUCATIONNUM   1.388249  1        1.178240
# CAPITALGAIN    1.018159  1        1.009038
# OCCUPATION_rep 1.531428  5        1.043541

library(car)

vif(logitMod)

# GVIF Df GVIF^(1/(2*Df))

# RELATIONSHIP 1.197104 5 1.018153

# AGE 1.089616 1 1.043847

# EDUCATIONNUM 1.388249 1 1.178240

# CAPITALGAIN 1.018159 1 1.009038

# OCCUPATION_rep 1.531428 5 1.043541

於是我們使用此模型來預測測試資料集。

prob <- predict(logitMod, testData, type="response")  # predicted scores

prob

為了優化模型正確率，我們使用InformationValue套件中的optimalCutoff函數來尋找最適機率切點。發現最適機率值切點跟預設的0.5一樣。

library(InformationValue)
optCutOff <- optimalCutoff(actuals = testData$ABOVE50K_y,predictedScores = predicted)[1]
optCutOff
# [1] 0.5

library(InformationValue)

optCutOff

# [1] 0.5

決定了機率切點後，我們來驗證模型使用測試資料集的預測效果如何。我們會分別計算以下指標：

Confusion Matrix
- misClassification Rate
- precision
- Sensitivity
- Specifisity
Concordance
ROC/AUC

Confusion Matrix: 左欄為預測值，上方欄則為實際值。

# 產生Confusion Matrix
confusionMatrix(actuals = testData$ABOVE50K_y,predictedScores = predicted,threshold = optCutOff)

#      0    1
# 0 6935 1074
# 1  481 1279

# 產生Confusion Matrix

confusionMatrix(actuals = testData$ABOVE50K_y,predictedScores = predicted,threshold = optCutOff)

# 0 1

# 0 6935 1074

# 1 481 1279

預測錯誤率(misClassification Rate)

misClassError(actuals = testData$ABOVE50K_y,predictedScores = predicted,threshold = optCutOff)
# [1] 0.1592

1 2	misClassError(actuals = testData$ABOVE50K_y,predictedScores = predicted,threshold = optCutOff) # [1] 0.1592

預測精準度(Precision，及所有預測為1的事件中，真實亦為1的事件比率）。

precision(actuals = testData$ABOVE50K_y,predictedScores = predicted,threshold = optCutOff)
# [1] 0.7267045

1 2	precision(actuals = testData$ABOVE50K_y,predictedScores = predicted,threshold = optCutOff) # [1] 0.7267045

Sensitivity

$$Sensitivity=\frac{\sharp\space Actual\space 1’s\space and\space Predicted\space as\space 1’s}{\sharp\space of\space Actual\space 1’s}$$

又稱Recall(捕捉率），即真實為1，且被正確預測為1的比例。（通常與Precision精準度成反比）

sensitivity(testData$ABOVE50K_y, predicted, threshold = optCutOff)
# [1] 0.5435614

1 2	sensitivity(testData$ABOVE50K_y, predicted, threshold = optCutOff) # [1] 0.5435614

Specificity

$$Specificity=\frac{\sharp\space Actual\space 0’s\space and\space Predicted\space as\space 0’s}{\sharp\space of\space Actual\space 0’s}$$

即真實為0，且被正確預測為0的比例。

specificity(testData$ABOVE50K_y, predicted, threshold = optCutOff)
# [1] 0.9351402

1 2	specificity(testData$ABOVE50K_y, predicted, threshold = optCutOff) # [1] 0.9351402

Concordance。則為所有預測結果(0,1)成對的機率值中，真實為1的事件，1的機率高於0的機率佔所有成對資料的比例。理想中，該比例越高越好，即表示所有預測(0,1)的機率值，若真實為1，則1的預測機率理應都大於0的預測機率。（discordance則為相反結果的比例，tied則為機率無差別的結果比例，三比例相加應為100%）。

Concordance(testData$ABOVE50K_y, predicted)

# $Concordance
# [1] 0.8866298
# 
# $Discordance
# [1] 0.1133702
# 
# $Tied
# [1] -0.00000000000000004163336
# 
# $Pairs
# [1] 17449848

Concordance(testData$ABOVE50K_y, predicted)

# $Concordance

# [1] 0.8866298

# $Discordance

# [1] 0.1133702

# $Tied

# [1] -0.00000000000000004163336

# $Pairs

# [1] 17449848

ROC/AUC。可以發現在ROC曲線下面積為88.85%。理想中，會希望ROC曲線前段越陡越好，後段越緩越好。表示模型整體預測能力的好壞。

plotROC(actuals = testData$ABOVE50K_y,predictedScores = predicted)

1	plotROC(actuals = testData$ABOVE50K_y,predictedScores = predicted)

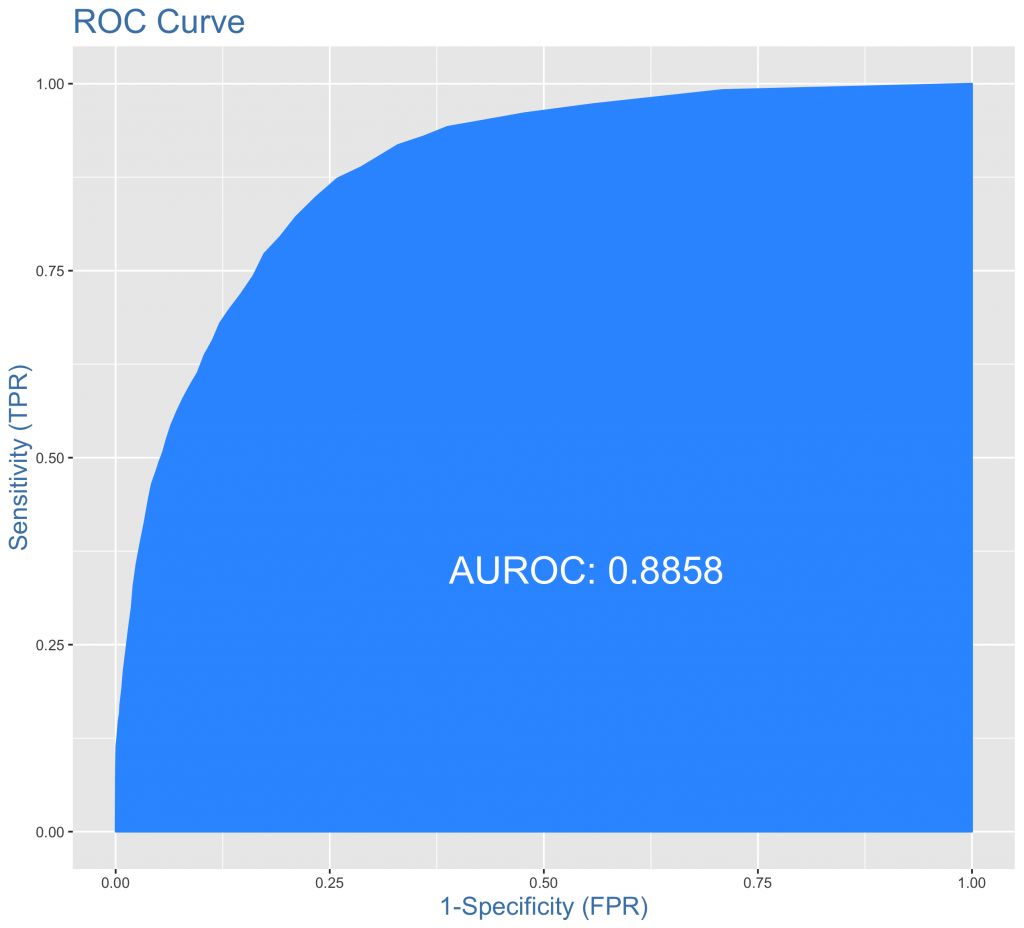
總結以上指標數據，可以發現模型預測能力還不錯，錯誤率15.92%都還在能接受範圍內。

7. 模型診斷與調整

為了近一步看看模型有無優化空間以及合適度，常見做法包括(1)殘差分析 (2)K-fold Cross Validation (3)Bootstrap (4)StepwiseRegression。我們這邊就以逐步回歸為範例，來看看模型是否有優化空間。

我們同時使用逐步向後/向前法，並比較兩法最後的結果(AIC)是否有差。

 為了進一步簡化模型，我們使用逐步向前/向後法來挑選變數
# 依據每一個變數加入/移除模型後AIC資訊的變化，來判斷變數對模型的效果
# full model設定為我們剛剛建模結果
m_full <- logitMod 
# 基礎只有截距的模型
m_null <- glm(formula = ABOVE50K_y ~ 1, family = binomial(link = "logit"),data = trainingData)

# backward selection 逐步向後法
stepModBack <- step(object = m_full,scope = list(lower = m_null, upper = m_full),direction = "backward",trace = F)
summary(stepModBack) #模型結果的AIC跟原始模型相同為15570

# Call:
#   glm(formula = ABOVE50K_y ~ RELATIONSHIP + AGE + EDUCATIONNUM + 
#         CAPITALGAIN + OCCUPATION_rep, family = binomial(link = "logit"), 
#       data = trainingData)
# 
# Deviance Residuals: 
#   Min       1Q   Median       3Q      Max  
# -5.2305  -0.5663  -0.2319  -0.0590   3.5991  
# 
# Coefficients:
#   Estimate  Std. Error z value
# (Intercept)                 -4.39303806  0.15173422 -28.952
# RELATIONSHIP Not-in-family  -2.34469608  0.05835820 -40.178
# RELATIONSHIP Other-relative -3.02210032  0.26185701 -11.541
# RELATIONSHIP Own-child      -3.72243110  0.16395790 -22.704
# RELATIONSHIP Unmarried      -2.66495726  0.09783246 -27.240
# RELATIONSHIP Wife           -0.00985696  0.07585158  -0.130
# AGE                          0.02285379  0.00171654  13.314
# EDUCATIONNUM                 0.30497481  0.01032637  29.534
# CAPITALGAIN                  0.00031083  0.00001181  26.312
# OCCUPATION_repBlue-Collar   -0.47777138  0.07013154  -6.813
# OCCUPATION_repOther/Unknown -1.33506791  0.13132122 -10.166
# OCCUPATION_repProfessional   0.16489267  0.07982984   2.066
# OCCUPATION_repService       -0.40645290  0.08448125  -4.811
# OCCUPATION_repWhite-Collar   0.24924877  0.06989076   3.566
# Pr(>|z|)    
# (Intercept)                 < 0.0000000000000002 ***
#   RELATIONSHIP Not-in-family  < 0.0000000000000002 ***
#   RELATIONSHIP Other-relative < 0.0000000000000002 ***
#   RELATIONSHIP Own-child      < 0.0000000000000002 ***
#   RELATIONSHIP Unmarried      < 0.0000000000000002 ***
#   RELATIONSHIP Wife                       0.896606    
# AGE                         < 0.0000000000000002 ***
#   EDUCATIONNUM                < 0.0000000000000002 ***
#   CAPITALGAIN                 < 0.0000000000000002 ***
#   OCCUPATION_repBlue-Collar       0.00000000000959 ***
#   OCCUPATION_repOther/Unknown < 0.0000000000000002 ***
#   OCCUPATION_repProfessional              0.038871 *  
#   OCCUPATION_repService           0.00000150055853 ***
#   OCCUPATION_repWhite-Collar              0.000362 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# (Dispersion parameter for binomial family taken to be 1)
# 
# Null deviance: 25162  on 22791  degrees of freedom
# Residual deviance: 15542  on 22778  degrees of freedom
# AIC: 15570
# 
# Number of Fisher Scoring iterations: 7


# forward selection 逐步向前法
stepModForward <- step(object = m_null,scope = list(lower = m_null, upper = m_full),direction = "forward",trace = F)
summary(stepModForward) 
# 向前法、向後法模型結果AIC值皆與原始模型相同為15570，且模型皆相同
# 因此我們會確定採用原始模型logigMod

# Call:
#   glm(formula = ABOVE50K_y ~ RELATIONSHIP + EDUCATIONNUM + CAPITALGAIN + 
#         OCCUPATION_rep + AGE, family = binomial(link = "logit"), 
#       data = trainingData)
# 
# Deviance Residuals: 
#   Min       1Q   Median       3Q      Max  
# -5.2305  -0.5663  -0.2319  -0.0590   3.5991  
# 
# Coefficients:
#   Estimate  Std. Error z value
# (Intercept)                 -4.39303806  0.15173422 -28.952
# RELATIONSHIP Not-in-family  -2.34469608  0.05835820 -40.178
# RELATIONSHIP Other-relative -3.02210032  0.26185701 -11.541
# RELATIONSHIP Own-child      -3.72243110  0.16395790 -22.704
# RELATIONSHIP Unmarried      -2.66495726  0.09783246 -27.240
# RELATIONSHIP Wife           -0.00985696  0.07585158  -0.130
# EDUCATIONNUM                 0.30497481  0.01032637  29.534
# CAPITALGAIN                  0.00031083  0.00001181  26.312
# OCCUPATION_repBlue-Collar   -0.47777138  0.07013154  -6.813
# OCCUPATION_repOther/Unknown -1.33506791  0.13132122 -10.166
# OCCUPATION_repProfessional   0.16489267  0.07982984   2.066
# OCCUPATION_repService       -0.40645290  0.08448125  -4.811
# OCCUPATION_repWhite-Collar   0.24924877  0.06989076   3.566
# AGE                          0.02285379  0.00171654  13.314
# Pr(>|z|)    
# (Intercept)                 < 0.0000000000000002 ***
#   RELATIONSHIP Not-in-family  < 0.0000000000000002 ***
#   RELATIONSHIP Other-relative < 0.0000000000000002 ***
#   RELATIONSHIP Own-child      < 0.0000000000000002 ***
#   RELATIONSHIP Unmarried      < 0.0000000000000002 ***
#   RELATIONSHIP Wife                       0.896606    
# EDUCATIONNUM                < 0.0000000000000002 ***
#   CAPITALGAIN                 < 0.0000000000000002 ***
#   OCCUPATION_repBlue-Collar       0.00000000000959 ***
#   OCCUPATION_repOther/Unknown < 0.0000000000000002 ***
#   OCCUPATION_repProfessional              0.038871 *  
#   OCCUPATION_repService           0.00000150055853 ***
#   OCCUPATION_repWhite-Collar              0.000362 ***
#   AGE                         < 0.0000000000000002 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# (Dispersion parameter for binomial family taken to be 1)
# 
# Null deviance: 25162  on 22791  degrees of freedom
# Residual deviance: 15542  on 22778  degrees of freedom
# AIC: 15570
# 
# Number of Fisher Scoring iterations: 7

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

為了進一步簡化模型，我們使用逐步向前/向後法來挑選變數

# 依據每一個變數加入/移除模型後AIC資訊的變化，來判斷變數對模型的效果

# full model設定為我們剛剛建模結果

m_full

# 基礎只有截距的模型

m_null

# backward selection 逐步向後法

stepModBack

summary(stepModBack) #模型結果的AIC跟原始模型相同為15570

# Call:

# glm(formula = ABOVE50K_y ~ RELATIONSHIP + AGE + EDUCATIONNUM +

# CAPITALGAIN + OCCUPATION_rep, family = binomial(link = "logit"),

# data = trainingData)

# Deviance Residuals:

# Min 1Q Median 3Q Max

# -5.2305 -0.5663 -0.2319 -0.0590 3.5991

# Coefficients:

# Estimate Std. Error z value

# (Intercept) -4.39303806 0.15173422 -28.952

# RELATIONSHIP Not-in-family -2.34469608 0.05835820 -40.178

# RELATIONSHIP Other-relative -3.02210032 0.26185701 -11.541

# RELATIONSHIP Own-child -3.72243110 0.16395790 -22.704

# RELATIONSHIP Unmarried -2.66495726 0.09783246 -27.240

# RELATIONSHIP Wife -0.00985696 0.07585158 -0.130

# AGE 0.02285379 0.00171654 13.314

# EDUCATIONNUM 0.30497481 0.01032637 29.534

# CAPITALGAIN 0.00031083 0.00001181 26.312

# OCCUPATION_repBlue-Collar -0.47777138 0.07013154 -6.813

# OCCUPATION_repOther/Unknown -1.33506791 0.13132122 -10.166

# OCCUPATION_repProfessional 0.16489267 0.07982984 2.066

# OCCUPATION_repService -0.40645290 0.08448125 -4.811

# OCCUPATION_repWhite-Collar 0.24924877 0.06989076 3.566

# Pr(>|z|)

# (Intercept)

# RELATIONSHIP Not-in-family

# RELATIONSHIP Other-relative

# RELATIONSHIP Own-child

# RELATIONSHIP Unmarried

# RELATIONSHIP Wife 0.896606

# AGE

# EDUCATIONNUM

# CAPITALGAIN

# OCCUPATION_repBlue-Collar 0.00000000000959 ***

# OCCUPATION_repOther/Unknown

# OCCUPATION_repProfessional 0.038871 *

# OCCUPATION_repService 0.00000150055853 ***

# OCCUPATION_repWhite-Collar 0.000362 ***

# ---

# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# (Dispersion parameter for binomial family taken to be 1)

# Null deviance: 25162 on 22791 degrees of freedom

# Residual deviance: 15542 on 22778 degrees of freedom

# AIC: 15570

# Number of Fisher Scoring iterations: 7

# forward selection 逐步向前法

stepModForward

summary(stepModForward)

# 向前法、向後法模型結果AIC值皆與原始模型相同為15570，且模型皆相同

# 因此我們會確定採用原始模型logigMod

# Call:

# glm(formula = ABOVE50K_y ~ RELATIONSHIP + EDUCATIONNUM + CAPITALGAIN +

# OCCUPATION_rep + AGE, family = binomial(link = "logit"),

# data = trainingData)

# Deviance Residuals:

# Min 1Q Median 3Q Max

# -5.2305 -0.5663 -0.2319 -0.0590 3.5991

# Coefficients:

# Estimate Std. Error z value

# (Intercept) -4.39303806 0.15173422 -28.952

# RELATIONSHIP Not-in-family -2.34469608 0.05835820 -40.178

# RELATIONSHIP Other-relative -3.02210032 0.26185701 -11.541

# RELATIONSHIP Own-child -3.72243110 0.16395790 -22.704

# RELATIONSHIP Unmarried -2.66495726 0.09783246 -27.240

# RELATIONSHIP Wife -0.00985696 0.07585158 -0.130

# EDUCATIONNUM 0.30497481 0.01032637 29.534

# CAPITALGAIN 0.00031083 0.00001181 26.312

# OCCUPATION_repBlue-Collar -0.47777138 0.07013154 -6.813

# OCCUPATION_repOther/Unknown -1.33506791 0.13132122 -10.166

# OCCUPATION_repProfessional 0.16489267 0.07982984 2.066

# OCCUPATION_repService -0.40645290 0.08448125 -4.811

# OCCUPATION_repWhite-Collar 0.24924877 0.06989076 3.566

# AGE 0.02285379 0.00171654 13.314

# Pr(>|z|)

# (Intercept)

# RELATIONSHIP Not-in-family

# RELATIONSHIP Other-relative

# RELATIONSHIP Own-child

# RELATIONSHIP Unmarried

# RELATIONSHIP Wife 0.896606

# EDUCATIONNUM

# CAPITALGAIN

# OCCUPATION_repBlue-Collar 0.00000000000959 ***

# OCCUPATION_repOther/Unknown

# OCCUPATION_repProfessional 0.038871 *

# OCCUPATION_repService 0.00000150055853 ***

# OCCUPATION_repWhite-Collar 0.000362 ***

# AGE

# ---

# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# (Dispersion parameter for binomial family taken to be 1)

# Null deviance: 25162 on 22791 degrees of freedom

# Residual deviance: 15542 on 22778 degrees of freedom

# AIC: 15570

# Number of Fisher Scoring iterations: 7

我們發現不管是逐步向前或向後法，最後結果都與原始logitMod的結果是一樣的。

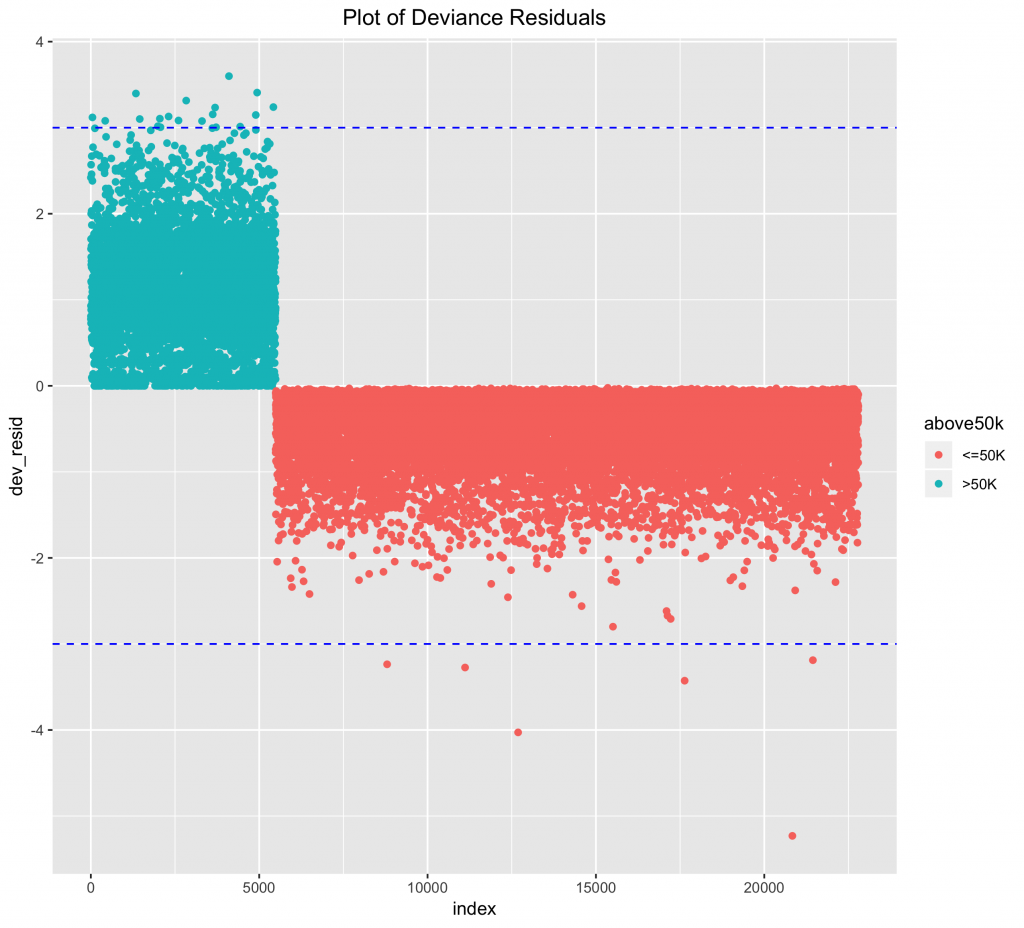
而理想中好的模型，偏差平方和(Deviance)應該在+-3之內，我們在此透過繪圖來檢視。

# 我們建立一個存放模型偏差殘差的資料表
index <- 1:dim(trainingData)[1]
# deviance residuals
dev_resid <- residuals(logitMod)
above50k <- trainingData$ABOVE50K
dff <- data.frame(index,dev_resid,above50k)

ggplot(data = dff, mapping = aes(x = index,y = dev_resid,color = above50k)) +
  geom_point() +
  geom_hline(yintercept = 3,linetype = "dashed", color = "blue") +
  geom_hline(yintercept = -3,linetype = "dashed", color = "blue") +
  labs(title = "Plot of Deviance Residuals") +
  theme(plot.title = element_text(hjust = 0.5))

# 我們建立一個存放模型偏差殘差的資料表

index

# deviance residuals

dev_resid

above50k

dff

ggplot(data = dff, mapping = aes(x = index,y = dev_resid,color = above50k)) +

geom_point() +

geom_hline(yintercept = 3,linetype = "dashed", color = "blue") +

geom_hline(yintercept = -3,linetype = "dashed", color = "blue") +

labs(title = "Plot of Deviance Residuals") +

theme(plot.title = element_text(hjust = 0.5))

可以發現偏差平方和皆都落在+-3範圍內(藍色虛線)。

8. 模型比較(v.s. Machine Learning Methods)

我們將傳統羅吉斯回歸預測結果與近期新穎的機器學習法預測結果做比較。

8-1. 類神經網路Neural Netwoarks(NN)

library(nnet)
# A formula of the form class ~ x1 + x2 + ...
# y should be "class"
nn1 <- nnet(as.factor(ABOVE50K_y) ~ RELATIONSHIP + AGE + EDUCATIONNUM + CAPITALGAIN + OCCUPATION_rep,
            data = trainingData,size = 40 , maxit = 500) 
# maxit: maximum number of iterations. Default 100.
# size: number of units in the hidden layer. Can be zero if there are skip-layer units.

# type只有"raw"=>prob, "class"=>0,1
nn1.predict <- predict(object = nn1,newdata = testData,type = "raw")

misClassError(actuals = testData$ABOVE50K_y,predictedScores = nn1.predict)
# [1] 0.1522 (<0.1592)

library(nnet)

# A formula of the form class ~ x1 + x2 + ...

# y should be "class"

nn1

data = trainingData,size = 40 , maxit = 500)

# maxit: maximum number of iterations. Default 100.

# size: number of units in the hidden layer. Can be zero if there are skip-layer units.

# type只有"raw"=>prob, "class"=>0,1

nn1.predict

misClassError(actuals = testData$ABOVE50K_y,predictedScores = nn1.predict)

# [1] 0.1522 (

類神經網路的預測分類錯誤率為15.22%，稍低於羅吉斯回歸的15.92%。

8-2. 決策樹CART

library(rpart)
tree2 <- rpart(formula = as.factor(ABOVE50K_y) ~ RELATIONSHIP + AGE + EDUCATIONNUM + CAPITALGAIN + OCCUPATION_rep,
               data = trainingData, method = "class",cp = 1e-3)
# 回傳每組預測0,1的機率結果
tree2.pred.prop <- predict(object = tree2, newdata = testData, type = "prob")
# 回傳預測0,1結果
tree2.pred <- predict(object = tree2,newdata = testData, type = "class")

# confusion Matrix
tb2 <- table(tree2.pred, testData$ABOVE50K_y)
tb2
# tree2.pred    0    1
#          0 6965 1022
#          1  451 1331

# missclassification rate
(1022+451) / (6965+1022+451+1331)
# [1] 0.1507831

library(rpart)

tree2

data = trainingData, method = "class",cp = 1e-3)

# 回傳每組預測0,1的機率結果

tree2.pred.prop

# 回傳預測0,1結果

tree2.pred

# confusion Matrix

tb2

# tree2.pred 0 1

# 0 6965 1022

# 1 451 1331

# missclassification rate

(1022+451) / (6965+1022+451+1331)

# [1] 0.1507831

決策樹的預測分類錯誤率為15.07%，低於羅吉斯回歸的15.92%。

8-3. 隨機森林Random Forest(RF)

# 透過產生bootstrapped的決策樹森林來優化模型預測正確率
library(randomForest)
rf3 <- randomForest(as.factor(ABOVE50K_y) ~ RELATIONSHIP + AGE + EDUCATIONNUM + CAPITALGAIN + OCCUPATION_rep,
                    data = trainingData, n_tree = 100)
rf3.pred.prob <- predict(object = rf3, newdata = testData, type = "prob")
rf3.pred <- predict(rf3, newdata = testData, type = "class")

# confusion matrix
tb3 <- table(rf3.pred, testData$ABOVE50K_y)
tb3

# rf3.pred    0    1
#        0 6908  968
#        1  508 1385

# missclassification rate
(968+508) / (6908+968+508+1385)
# [1] 0.1510902

# 透過產生bootstrapped的決策樹森林來優化模型預測正確率

library(randomForest)

rf3

data = trainingData, n_tree = 100)

rf3.pred.prob

rf3.pred

# confusion matrix

tb3

# rf3.pred 0 1

# 0 6908 968

# 1 508 1385

# missclassification rate

(968+508) / (6908+968+508+1385)

# [1] 0.1510902

隨機森林的預測分類錯誤率為15.11%，低於羅吉斯回歸的15.92%。

8-4. 支援向量機Support Vector Machine(SVM)

library(kernlab)
svm4 <- ksvm(as.factor(ABOVE50K_y) ~ RELATIONSHIP + AGE + EDUCATIONNUM + CAPITALGAIN + OCCUPATION_rep,data = trainingData)
svm4.pred.prob <- predict(svm4,testData, type = "decision")
svm4.pred <- predict(svm4,testData, type = "response")

tb4 <- table(svm4.pred, testData$ABOVE50K_y)
tb4

# svm4.pred    0    1
#         0 6976 1060
#         1  440 1293

# missclassification rate
(440+1060) / (6976+1060+440+1293)
# [1] 0.1535469

library(kernlab)

svm4

svm4.pred.prob

svm4.pred

tb4

# svm4.pred 0 1

# 0 6976 1060

# 1 440 1293

# missclassification rate

(440+1060) / (6976+1060+440+1293)

# [1] 0.1535469

SVM的預測分類錯誤率為15.35%，亦低於羅吉斯回歸的15.92%。

綜合以上結果，我們摘要傳統羅吉斯回歸與機器學習法的預測結果如下表：

演算法	預測錯誤率
傳統羅吉斯回歸	15.92%
類神經網路	15.22%
決策樹(CART)	15.11%
支持向量機(SVM)	15.35%

可以發現機器學習法的對所有測試資料的預測錯誤率沒有比傳統羅吉斯回歸差距太大。

Confusion Matrix看的是模型對於所有data的預測正確度(accuracy)，但因為我們的大部分的資料都是<=50K，所以我們更會比較在不同資料使用水平下，模型在正確度的表現。我們在此會使用ROC曲線及曲線下面積AUC來看比較五個模型分別在不同資料水平下的模型預測正確率(accuracy)表現。

先載入套件ROCR。並替所有模型預測結果產生一組放置(X軸)False Positive Rate和(Y軸)True Positive Rate的data frame，以便後續繪製各模型的ROC曲線。

首先是Logistic Regression的部份如下：

library(ROCR)

# logistic regression:
# 使用ROC評估分類模型前，都會先創造一個prediction物件，用來將輸入資料標準化
# predictions 為使用測試資料集的模型(logitMod)預測結果(probabilities)，
# 而labels為真實測試集的資料類別(category)
# 兩者個維度必須相同
pr <- prediction(predictions = prob, labels = testData$ABOVE50K_y)
# 產生成效物件。所有的預測評估都會使用這個函數。measure為y軸指標，x.measure為x軸指標。
# 這邊我們會放上ROC曲線的x軸和y軸資訊，分別為1-specificity(x.measure)和sensitivity/recall(measure)
prf <- performance(prediction.obj = pr,measure = "tpr", x.measure = 'fpr')
# 建立一個TP rate和FP rate的data frame
dd <- data.frame(FP = prf@x.values[[1]], TP = prf@y.values[[1]])

library(ROCR)

# logistic regression:

# 使用ROC評估分類模型前，都會先創造一個prediction物件，用來將輸入資料標準化

# predictions 為使用測試資料集的模型(logitMod)預測結果(probabilities)，

# 而labels為真實測試集的資料類別(category)

# 兩者個維度必須相同

# 產生成效物件。所有的預測評估都會使用這個函數。measure為y軸指標，x.measure為x軸指標。

# 這邊我們會放上ROC曲線的x軸和y軸資訊，分別為1-specificity(x.measure)和sensitivity/recall(measure)

prf

# 建立一個TP rate和FP rate的data frame

其他機器學習法如法炮製如下：

# Neural Networks (NN):
pr1 <- prediction(predictions = nn1.predict,labels = testData$ABOVE50K_y)
prf1 <- performance(prediction.obj = pr1,measure = "tpr",x.measure = "fpr")
dd1 <- data.frame(FP = prf1@x.values[[1]], TP = prf1@y.values[[1]])

# CART:
pr2 <- prediction(predictions = tree2.pred.prop[,2], labels = testData$ABOVE50K_y)
prf2 <- performance(prediction.obj = pr2,measure = "tpr", x.measure = "fpr")
dd2 <- data.frame(FP = prf2@x.values[[1]], TP = prf2@y.values[[1]])

# Random Forest (RF):
pr3 <- prediction(predictions = rf3.pred.prob[,2],labels = testData$ABOVE50K_y)
prf3 <- performance(prediction.obj = pr3, measure = "tpr", x.measure = "fpr")
dd3 <- data.frame(FP = prf3@x.values[[1]], TP = prf3@y.values[[1]])

# SVM:
pr4 <- prediction(predictions = svm4.pred.prob,labels = testData$ABOVE50K_y)
prf4 <- performance(prediction.obj = pr4,measure = "tpr", x.measure = "fpr")
dd4 <- data.frame(FP = prf4@x.values[[1]], TP = prf4@y.values[[1]])

# Neural Networks (NN):

pr1

prf1

dd1

# CART:

pr2

prf2

dd2

# Random Forest (RF):

pr3

prf3

dd3

# SVM:

pr4

prf4

dd4

準備好各模型預測結果dd, dd1, ~ ,dd4的data frame後，我們將他們轉換成ROC曲線。

# 將以上幾個模型的ROC曲線畫出：
library(ggplot2)
g <- 
  ggplot() +
    geom_line(data = dd,mapping = aes(x = FP, y = TP, color = 'Logistic Regression')) +
    geom_line(data = dd1,mapping = aes(x = FP, y = TP, color = 'Neural Networks')) +
    geom_line(data = dd2,mapping = aes(x = FP, y = TP, color = 'CART')) +
    geom_line(data = dd3,mapping = aes(x = FP, y = TP, color = 'Random Forest')) +
    geom_line(data = dd4,mapping = aes(x = FP, y = TP, color = 'Support Vector Machine')) +
    geom_segment(mapping = aes(x = 0, xend = 1, y = 0, yend = 1)) +
    ggtitle(label = "ROC Curve") +
    labs(x = "False Positive Rate", y = "True Positive Rate")
g +
  scale_color_manual(name = "classifier",values = c('Logistic Regression'='#E69F00', 
                                                    'Neural Networks'='#56B4E9', 'CART'='#009E73', 
                                                    'Random Forest'='#D55E00', 'Support Vector Machine'='#0072B2'))

# 將以上幾個模型的ROC曲線畫出：

library(ggplot2)

ggplot() +

geom_line(data = dd,mapping = aes(x = FP, y = TP, color = 'Logistic Regression')) +

geom_line(data = dd1,mapping = aes(x = FP, y = TP, color = 'Neural Networks')) +

geom_line(data = dd2,mapping = aes(x = FP, y = TP, color = 'CART')) +

geom_line(data = dd3,mapping = aes(x = FP, y = TP, color = 'Random Forest')) +

geom_line(data = dd4,mapping = aes(x = FP, y = TP, color = 'Support Vector Machine')) +

geom_segment(mapping = aes(x = 0, xend = 1, y = 0, yend = 1)) +

ggtitle(label = "ROC Curve") +

labs(x = "False Positive Rate", y = "True Positive Rate")

g +

scale_color_manual(name = "classifier",values = c('Logistic Regression'='#E69F00',

'Neural Networks'='#56B4E9', 'CART'='#009E73',

'Random Forest'='#D55E00', 'Support Vector Machine'='#0072B2'))

從圖中可以觀察到，模型中以Neural Networks表現最好，及能使用最少的資料，可以捕捉到最多的目標事件1。(理想中，ROC曲線前段越陡越好，後段則越緩越佳）。

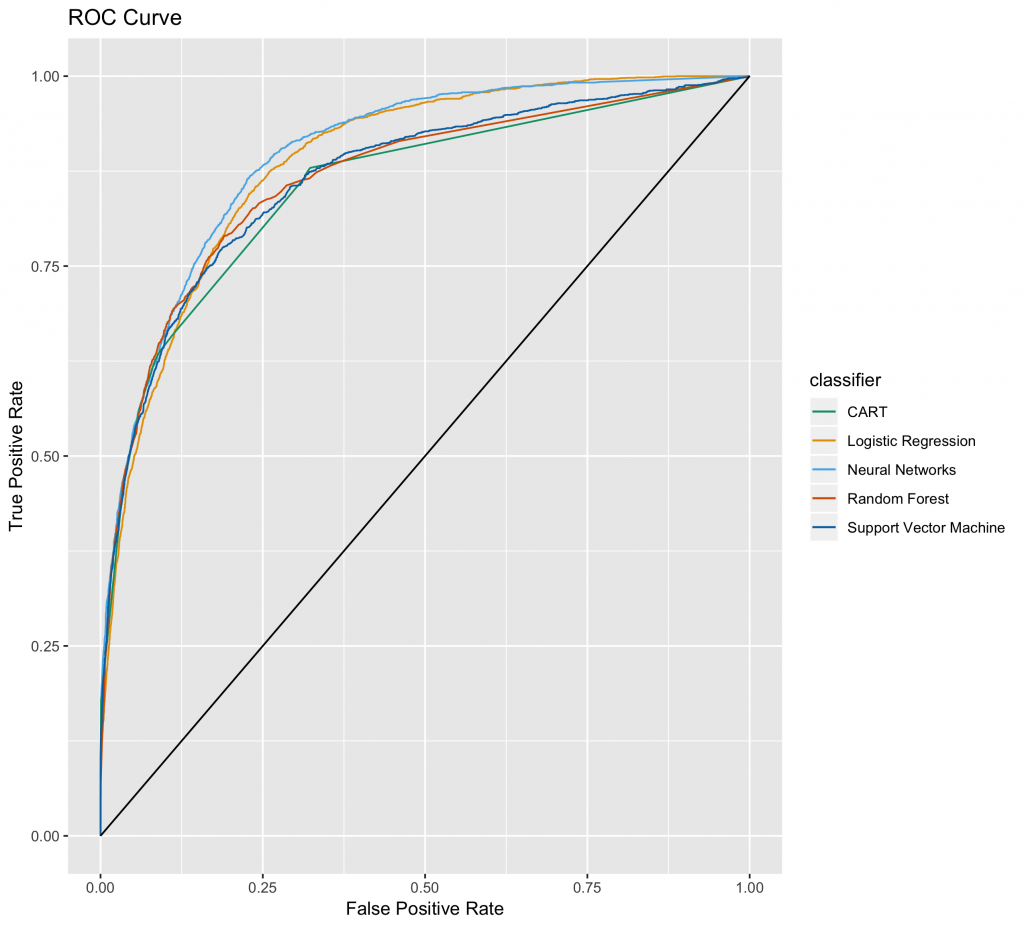
我們進一步將ROC曲線下面積AUC計算出來。

# AUC
auc <- 
  rbind(performance(pr, measure = 'auc')@y.values[[1]],
        performance(pr1, measure = 'auc')@y.values[[1]],
        performance(pr2, measure = 'auc')@y.values[[1]],
        performance(pr3, measure = 'auc')@y.values[[1]],
        performance(pr4, measure = 'auc')@y.values[[1]])

rownames(auc) <- (c('Logistic Regression', 'Neural Networks', 'CART',
                    'Random Forest', 'Support Vector Machine'))
colnames(auc) <- 'Area Under ROC Curve'
round(auc, 4)

#                        Area Under ROC Curve
# Logistic Regression                  0.8868
# Neural Networks                      0.8970
# CART                                 0.8543
# Random Forest                        0.8646
# Support Vector Machine               0.8651

# AUC

auc

rbind(performance(pr, measure = 'auc')@y.values[[1]],

performance(pr1, measure = 'auc')@y.values[[1]],

performance(pr2, measure = 'auc')@y.values[[1]],

performance(pr3, measure = 'auc')@y.values[[1]],

performance(pr4, measure = 'auc')@y.values[[1]])

rownames(auc)

'Random Forest', 'Support Vector Machine'))

colnames(auc)

round(auc, 4)

# Area Under ROC Curve

# Logistic Regression 0.8868

# Neural Networks 0.8970

# CART 0.8543

# Random Forest 0.8646

# Support Vector Machine 0.8651

可以發現，Neural Networks曲線下面積最高，Logistic Regression則次之。但因為類神經網路有諸多黑箱邏輯，故為了有更多的解釋基礎，一般來說，還是會選擇使用羅吉斯回歸結果來說明。從此範例也可發現，傳統羅吉斯回歸的對此資料集的預測能力並不亞於諸多新穎的機器學習法。

總結

羅吉斯回歸與回歸模型相似，必須符合許多基本假設，也因此對資料分配有較多要求，資料前處理的需求亦較多（遺失值、離群值、資料分佈）。
回歸模型基本上並不包含變數篩選，所以事前會使用IV(information value)來做變數初步篩選，事後也會使用VIF檢視共線性。
和線性回歸一樣，羅吉斯會將類別型變數轉換成虛擬變數，因此要避免類別水準值過多的情形。
評估模型適合度，需綜合考量整體錯誤率(misclassification rate)與在不同資料量水平下的捕捉率(ROC/AUC)。
羅吉斯回歸適合用來預測類別變數（二元變數）的機率。
模型調整的工約80%是在於資料前處理。

更多模型建置筆記連結：

參考:

歐萊禮 R資料科學