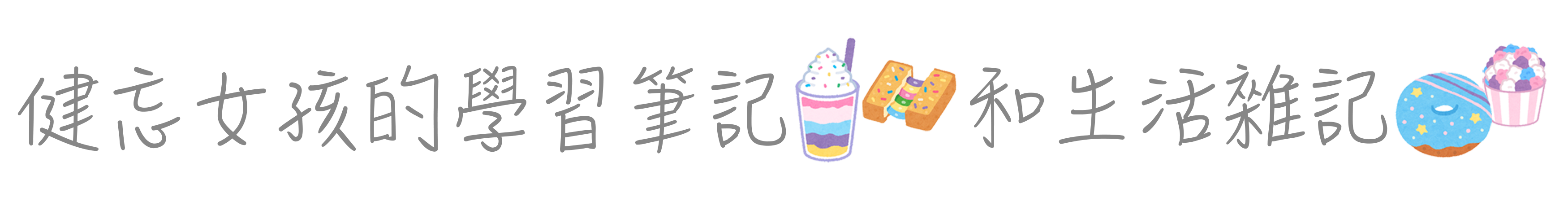Random Forests 隨機森林 | randomForest, ranger, h2o

Bagging法綜合多個樹模型結果，可以降低單一樹模型的高變異性並提升預測正確率。但Bagging法中樹與樹之間的相關性會降低模型整體的表現。隨機森林 Random forests 是Bagging修改後的版本，它是由「去相關性」的樹模型所組成的集成演算法，有很不錯的預測正確率且是一個受歡迎、開箱即用的演算法。

載入所需套件

library(rsample)      # data splitting 
library(randomForest) # basic implementation
library(ranger)       # a faster implementation of randomForest
library(caret)        # an aggregator package for performing many machine learning models
library(h2o)          # an extremely fast java-based platform
library(dplyr)
library(magrittr)

library(rsample) # data splitting

library(randomForest) # basic implementation

library(ranger) # a faster implementation of randomForest

library(caret) # an aggregator package for performing many machine learning models

library(h2o) # an extremely fast java-based platform

library(dplyr)

library(magrittr)

準備資料。

使用AmesHousing套件中的Ames Housing Data。
使用resample package中的initial_split()將資料切分成7:3(將參數設定為prop = 0.7)。
再分別用training()和testing()函數將切分好的資料萃取出。
並使用set.seed()來確保資料切分結果是可再現的。

# Create training (70%) and test (30%) sets for the AmesHousing::make_ames() data.
# Use set.seed for reproducibility
set.seed(123)
ames_split <- initial_split(data = AmesHousing::make_ames(), prop = .7)
ames_train <- training(ames_split)
ames_test  <- testing(ames_split)

# Create training (70%) and test (30%) sets for the AmesHousing::make_ames() data.

# Use set.seed for reproducibility

set.seed(123)

ames_split

ames_train

ames_test

Random Forests 概念介紹

隨機森林模型的基礎概念和Decision Trees和Bagging一樣的(可以參考決策樹,Decision Trees和Bagging)。Bagging Trees模型在演算法中納入了隨機的元素，有效的降低了單一樹模型的高變異性與提升模型預測正確率。然而在bagging中的trees並非所有都是彼此相互獨立的，因為在每一棵樹切分節點時都是考慮所有原始的預測變數。也因爲上述關係，來自不同bootstrapped samples的樹彼此的結構都會有些類似（尤其是在樹的上半部，用來切割的前幾大變數都會非常類似）。

樹的結構相遇的這個特性就稱作tree correlation，它阻礙了Bagging最適地降低預測目標值的變異(variance)。為了更近一步降低變異，我們需要最小化樹與樹之間的相關性。這可以透過注入更多的隨機性到長樹的過程。 Random Forests是透過以下兩步驟來達成的：

Bootstrap (拔靴法) : 跟Bagging很類似，每一顆樹都是建立自不同的bootstrapped sample，讓他們稍稍不一樣並稍稍去相關性。
Split-variable randomization (變數切割的隨機性) : 每一次在執行變數切割時，搜尋切割變數的範圍被限縮為隨機的子集合，即隨機挑選m個隸屬於總p個變數的子集合作為切割搜尋變數的範圍。對回歸樹來說，預設使用$m=\frac{p}{3}$，是個可經調教的參數。當$m = p$的時候，則跟只進行步驟1的結果一樣。

因為每棵樹都是來自不同的隨機bootstrapped sample且每一次切割都是隨機挑選變數的子集合，因此樹與樹之間的關聯性會下降地較Bagging更低。

OOB error vs. test set error

和Bagging一樣，bootstrap resample法的一個天然好處，就是隨機森林模型可以透過out-of-bag(OOB)的樣本誤差來作為有效與合理近似實驗誤差(test error)。不需要額外產生或犧牲訓練資料集，OOB sample可供作為一個內建的驗證子集合。OOB sample 的存在讓尋找使模型錯誤率趨於穩定的最適樹模型數量(ntree)更有效率。但是OOB error和test error終究還是預期會不太相同。

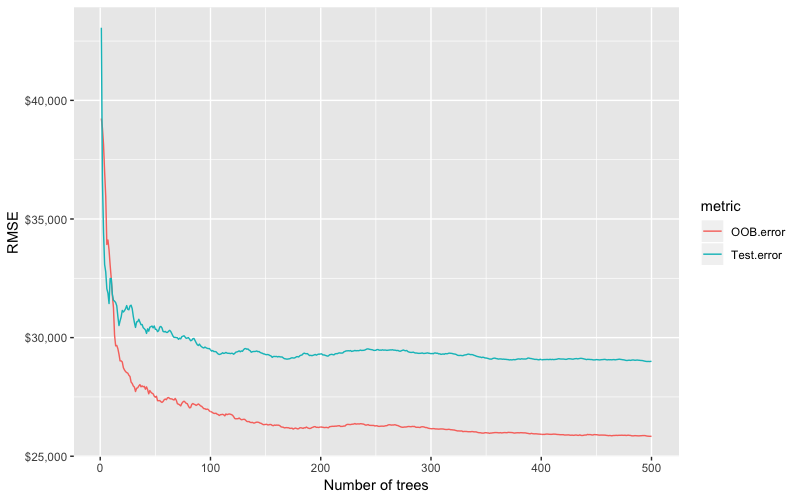
[上圖：Random forest out-of-bag error versus validation error.]

此外，有很多package都沒有可以追蹤在某一棵樹模型中，哪些是OOB sample哪些不是的功能。這樣在比須比較多個模型的成效時，想要使用相同的驗證資料集來幫每個模型打分數是不可行的。而且，技術上雖然可以對OOB sample計算特定指標(metrics)如root mean squared logarithmic error (RMSLE)，但並非所有package都有內建這樣的運算功能。所以如果你想要比較多個模型的成效或是使用較不傳統的損失函數指標，你可能還是會選擇cross validation。

Advantages & Disadvantages of Random Forests

優點

隨機森林模型通常具有非常好的成效。
非常好的「開箱即用」的模型-不太需要調整什麼參數。
有內建的驗證資料集validation set – 不須為了額外驗證而犧牲資料。
不需前處理(pre-processing)。
對於離群值的處理是強大的。

缺點

當運算大型資料時會變的非常慢。
雖然模型預測正確率高，但通常無法跟更先進的boosting演算法相比。
較不易解釋。

基本實作

在R中有超過20種的Random Forests Packages。以下會使用歷史最悠久且最受歡迎randomForest套件來說明示範基本的Random Forests模型實作。但必須注意，當你的資料集變得很大的時候，randomForest回無法很好的擴展到大型資料（即使使用foreach進行平行運算）。此外，為了探索和比較不同模型參數的效果，我們也可找到更多有效的套件。因此，在模型tuning階段，我們會說明如何使用ranger和h2o package來進行更有效率的Random Forests modeling。

randomForest::randomForest可以使用formula或x,y matrix表示的方式來指定模型資料。我們以下以formula的方式來指定模型設定並使用randomForest模型預設參數。

# for reproduciblity
set.seed(123)

# default RF model
m1 <- randomForest(
  formula = Sale_Price ~ .,
  data    = ames_train
)

m1

# for reproduciblity

set.seed(123)

# default RF model

formula = Sale_Price ~ .,

data = ames_train

)

## 
## Call:
##  randomForest(formula = Sale_Price ~ ., data = ames_train) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 26
## 
##           Mean of squared residuals: 661089658
##                     % Var explained: 89.8

## Call:

## randomForest(formula = Sale_Price ~ ., data = ames_train)

## Type of random forest: regression

## Number of trees: 500

## No. of variables tried at each split: 26

## Mean of squared residuals: 661089658

## % Var explained: 89.8

從m1結果來看：

randomForest預設會使用500棵樹。
每一次切割(each split)會隨機篩選出$\frac{Features}{3}=26$個預測變數作為base。(原始data扣除目標變數Sale_Price的number of features = 80)
m1$mse(regression only)代表的是由OOB sample所計算出的「平均誤差平方(mean squared erre)」向量，即殘差平方和(sum of squared residuals)除上樹的個數(n)。
綜合500棵樹的mse(OOB error)為m1$mse[500] = 6.6108966 × 10⁸。

我們可以進一步將不同棵樹所組成的隨機森林模型(ntree)對應的平均誤差(MSE)給繪出：

plot(m1)

plot(m1)

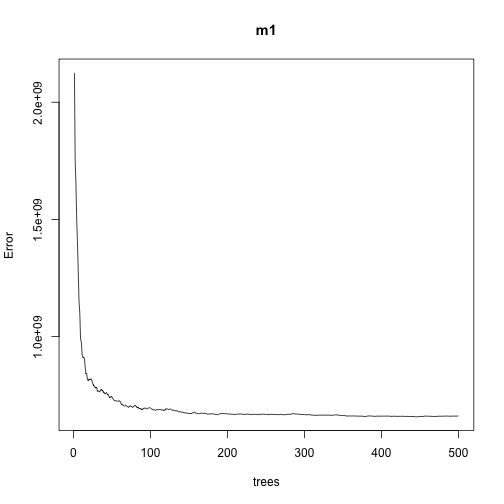
從上圖可以發現，模型平均誤差大概在100棵樹時開始趨於穩定，且平均誤差值降低的速度開始於300棵樹左右時開始變緩。

我們可以進一步找出使得MSE最小的樹的個數。

which.min(m1$mse)

1	which.min(m1$mse)

## [1] 447

1 2	## [1] 447

最適隨機森林的RMSE則為(平均Sale_Price的誤差值)：

sqrt(m1$mse[which.min(m1$mse)])

1	sqrt(m1$mse[which.min(m1$mse)])

## [1] 25648.78

1 2	## [1] 25648.78

如果我們不想要OOB error，randomForest函數亦提供驗證資料集(validation set)來幫助我們計算模型預測正確率。

要計算驗證誤差，首先我們進一步將訓練資料集依據8:2的比例切成訓練和驗證資料集，並分別使用analysis()和assessment()函數萃取出訓練和驗證資料。

# create training and validation data 
set.seed(123)
valid_split <- initial_split(ames_train, .8)

# training data
ames_train_v2 <- analysis(valid_split)

# validation datas
ames_valid <- assessment(valid_split)

# 將驗證資料整理成x_test和y_test
x_test <- ames_valid[setdiff(names(ames_valid),"Sale_Price")]
y_test <- ames_valid$Sale_Price

# 在randomForest函數中使用x-test和y-test當作驗證資料集的參數
rf_oob_comp <- randomForest(
  formula = Sale_Price ~ .,
  data = ames_train_v2,
  xtest = x_test,
  ytest = y_test
)

rf_oob_comp

# create training and validation data

set.seed(123)

valid_split

# training data

ames_train_v2

# validation datas

ames_valid

# 將驗證資料整理成x_test和y_test

x_test

y_test

# 在randomForest函數中使用x-test和y-test當作驗證資料集的參數

rf_oob_comp

formula = Sale_Price ~ .,

data = ames_train_v2,

xtest = x_test,

ytest = y_test

)

rf_oob_comp

## 
## Call:
##  randomForest(formula = Sale_Price ~ ., data = ames_train_v2,      xtest = x_test, ytest = y_test) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 26
## 
##           Mean of squared residuals: 667486651
##                     % Var explained: 89.17
##                        Test set MSE: 841004412
##                     % Var explained: 89.16

## Call:

## randomForest(formula = Sale_Price ~ ., data = ames_train_v2, xtest = x_test, ytest = y_test)

## Type of random forest: regression

## Number of trees: 500

## No. of variables tried at each split: 26

## Mean of squared residuals: 667486651

## % Var explained: 89.17

## Test set MSE: 841004412

## % Var explained: 89.16

可以看到模型結果多了Test set MSE，和原始的OOB MES不太一樣。我們將不同顆樹組成的模型所對應的OOB error和test error萃取出來並畫出誤差隨著樹的數量的變化圖，並比較兩者的差距。

# extract OOB & validation errors
oob <- sqrt(rf_oob_comp$mse)
validation <- sqrt(rf_oob_comp$test$mse)

data.frame(
  ntrees = 1:rf_oob_comp$ntree,
  OOB.error = oob,
  Test.error = validation
) %>% 
  gather(key = metric, value = RMSE, 2:3) %>% 
  ggplot(aes(x = ntrees, y = RMSE, color = metric)) +
  geom_line() +
  scale_y_continuous(labels = scales::dollar) +
  xlab("Number of trees")

# extract OOB & validation errors

oob

validation

data.frame(

ntrees = 1:rf_oob_comp$ntree,

OOB.error = oob,

Test.error = validation

) %>%

gather(key = metric, value = RMSE, 2:3) %>%

ggplot(aes(x = ntrees, y = RMSE, color = metric)) +

geom_line() +

scale_y_continuous(labels = scales::dollar) +

xlab("Number of trees")

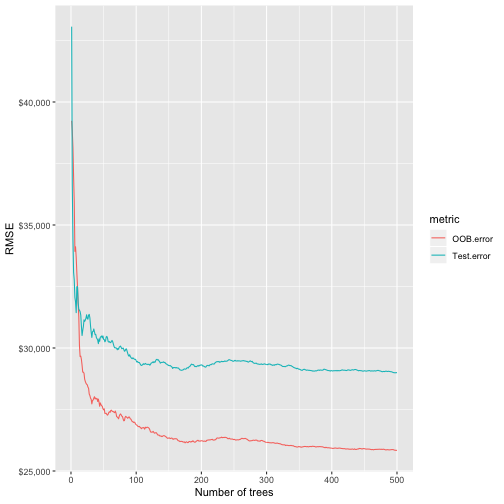
Random Forests是其中一個很好的「開箱即用」的演算法之一。基本上不需要調整什麼參數(tuning)，模型的預測能力就可ㄧ有很好的成效。

舉例來說，從上圖中，我們不需要調整參數就可以得到小於$30K的RMSE，比完整tuning後的Bagging模RMSE降低超過$6K；比完整tuning的elastic net模型RMSE降低超過$2K(沒有將目標變數取log的elastic net model版本請參考以下)。而我們還可以進一步透過參數調整tuning將Random Forests模型的預測正確性優化。

# elastic net
library(caret)
ames_train_x <- model.matrix(object = Sale_Price ~ ., data =  ames_train)[, -1]
ames_train_y <- ames_train$Sale_Price

# ames_test_x <- model.matrix(Sale_Price ~ ., ames_test)[, -1]
# ames_test_y <- ames_test$Sale_Price

train_control <- trainControl(method = "cv", number = 10)

caret_mod <- train(
  x = ames_train_x, 
  y = ames_train_y,
  method = "glmnet", 
  prePro = c("center","scale","zv","nzv"),
  trControl = train_control,
  tuneLength = 10
)

min(caret_mod$results$RMSE)

# elastic net

library(caret)

ames_train_x

ames_train_y

# ames_test_x

# ames_test_y

train_control

caret_mod

x = ames_train_x,

y = ames_train_y,

method = "glmnet",

prePro = c("center","scale","zv","nzv"),

trControl = train_control,

tuneLength = 10

)

min(caret_mod$results$RMSE)

## [1] 32268.14

1 2	## [1] 32268.14

tuning

Random Forests在tuning上非常簡單，因為只有幾個tuning parameters。通常tuning模型一開始最主要的考量點就是每一次分割所用來挑選的潛在變數名單，另外就是幾個需要注意的hyperparameters，包括如下：(這些hyperparameters在不同package的命名可能有所不同)

ntree : number of trees。我們希望有足夠的樹來穩定模型的誤差，但過多的樹會是沒效率且沒必要的，特別是遇到大型資料集的時候。
mtry : 每次在決定切割變數時，所隨機抽樣的潛在變數清單數量。當mtry = p(即所有特徵變數數量)，Random Forests的結果就會和bagging一樣。而當mtry = 1，會造就每一次split所使用的變數completely random，每個變數都有機會但會造成非常偏差的結果。
sampsize : 訓練每棵樹模型的樣本數大小。預設是使用63.25%訓練資料集的比例，因為這個是獨立觀察值出現在bootstrapped sample的期望機率值。較低的樣本數大小雖然會降低訓練時間，但可能會產生不必要的偏差。增加樣本數大小可以提升模型正確率，但有可能會產生overfitting(因為會增加模型變異性)。所以一般來說，我們校正此樣本大小參數時會使用60-80%的比例。
nodesize : 末梢(葉)節點最小觀察資料個數。用來控制樹模型的複雜度。小的葉節點大小允許更深更複雜的樹模型，大的葉節點大小則會產生叫淺的樹模型。這又是一種「偏差v.s.變異度(bias -variance)」的權衡，當樹長得越深時，模型變異性愈高(有過度配適的風險)，而當樹長得越潛時則會有較多偏差(有沒辦法完整捕捉資料中的模式跟關係)。
maxnode : 內部節點最大個數值。另一種控制模型複雜度的變數，內部節點樹越多則會長出更深的樹，內部節點越少則產生越淺的樹。

Initial tuning with randomForest

如果一開始只針對mtry進行校正，可以使用randomForest::tuneRF來進行簡易快速的評估。tunRF會從指定的mtry值開始，並每次增加給定的間距，直到模型OOB error降低的幅度開始小於特定幅度為止。

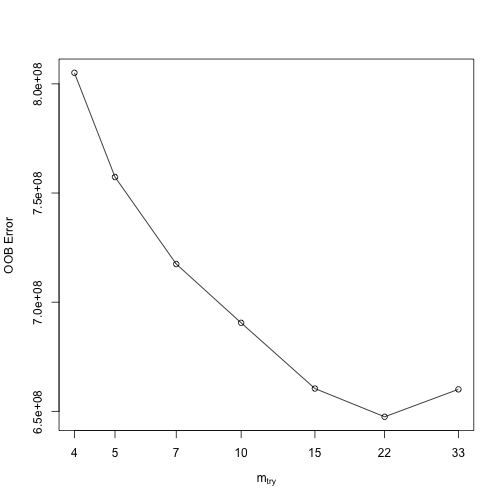
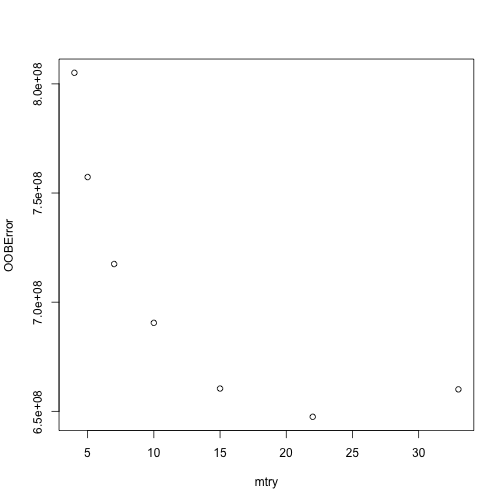
比如說，以下想知道mtry從5開始，每間隔相加1.5，所得到到的OOB error，直到OOB error改善的不度不超過1%為止。

因為tuneRF需要使用x,y形式指定資料，因此首先我們先使用setdiff()函數將變數名稱依據目標變數與預測變數分開。

模型跑完後會自動將每個mtry值所對應的OOB error值繪出。我們可以發現，當mtry > 22後，OOB開始不再下降，最適mtry水準值約與features/3 = 80/3 = 26差不多。

# 篩選出預測變數名稱
features <- setdiff(x = names(ames_train), y = "Sale_Price")

# 固定不同mtry參數值的模型所使用的隨機OOB sample一樣的
set.seed(123)

m2 <- tuneRF(x = ames_train[features], y = ames_train$Sale_Price, mtryStart = 5, ntreeTry = 500 ,stepFactor = 1.5, improve = 0.01, trace = FALSE)

# 篩選出預測變數名稱

features

# 固定不同mtry參數值的模型所使用的隨機OOB sample一樣的

set.seed(123)

plot(m2)

plot(m2)

Full grid search with ranger

如果想要套用綜合mtry以及其他參數的hyperparameter組合，我們需要建立一個grid並使用loop迴圈的方式，去測試每一個hyperparameter的組合和模型的成效。但因為randomForest()函數無法有效的將運算擴展至大型數據運算，因此我們會使用以c++執行的ranger()函數來解決。

我們可先使用Sys.time()稍稍比較tuneRF和ranger執行一種隨機森林模型所需的時間。

system.time(
  ames_randomForest <- randomForest(
    formula = Sale_Price ~ ., 
    data = ames_train, 
    ntree = 500, 
    mtry = floor(length(features)/3)
  )
)

system.time(

ames_randomForest

formula = Sale_Price ~ .,

data = ames_train,

ntree = 500,

mtry = floor(length(features)/3)

)

##    user  system elapsed 
## 111.957   0.735 169.989

## user system elapsed

## 111.957 0.735 169.989

system.time(
  ames_ranger <- ranger(
    formula   = Sale_Price ~ ., 
    data      = ames_train, 
    num.trees = 500,
    mtry      = floor(length(features) / 3)
  )
)

system.time(

ames_ranger

formula = Sale_Price ~ .,

data = ames_train,

num.trees = 500,

mtry = floor(length(features) / 3)

)

##    user  system elapsed 
##  10.367   0.174   5.665

## user system elapsed

## 10.367 0.174 5.665

由以上結果我們可以看到，同樣是執行一次隨機森林，ranger()所需的時間僅約6秒，而randomForests則需要169秒。

為了進行grid search，我們首先先建立一個hyperparameters的grid，由許多不同的mtry, minimum node size,和 sample size所組成。總共會有96種組合。

# hyperparameter grid search
hyper_grid <- expand.grid(
  mtry = seq(20, 30, by = 2),
  node_size = seq(3, 9, by = 2),
  sample_size = c(0.55, 0.632, 0.7, 0.8),
  OOB_RMSE = 0
)

# total number of combinations
nrow(hyper_grid)

# hyperparameter grid search

hyper_grid

mtry = seq(20, 30, by = 2),

node_size = seq(3, 9, by = 2),

sample_size = c(0.55, 0.632, 0.7, 0.8),

OOB_RMSE = 0

)

# total number of combinations

nrow(hyper_grid)

## [1] 96

## [1] 96

我們使用loop迴圈，一一帶入不同hyperparameters到ranger()函數中，並固定每一次randomForests的的森林樹木數量為500(因為從前面經驗我們知道500棵樹即足夠使OOB error趨於穩定並收斂)。另外每一次randomForests執行時，我們也固定隨機亂數種子，讓同樣sample_size參數值所對應的抽樣樣本可以相同，凸顯其他參數變化所帶來的效果。

for (i in 1:nrow(hyper_grid)) {
  # train model
  model <- ranger(
    formula = Sale_Price ~ .,
    data = ames_train, 
    num.trees = 500, 
    mtry = hyper_grid$mtry[i],
    min.node.size = hyper_grid$node_size[i], 
    sample.fraction = hyper_grid$sample_size[i],
    seed = 123
  )

  # 並將每一此訓練模型的OOB RMSE萃取儲存
  hyper_grid$OOB_RMSE[i] <- sqrt(model$prediction.error)
}

# 我們將結果依序OOB_RMSE由小至大排列，取模型成效前十名印出
hyper_grid %>% 
  dplyr::arrange(OOB_RMSE) %>% 
  head(10)

for (i in 1:nrow(hyper_grid)) {

# train model

model

formula = Sale_Price ~ .,

data = ames_train,

num.trees = 500,

mtry = hyper_grid$mtry[i],

min.node.size = hyper_grid$node_size[i],

sample.fraction = hyper_grid$sample_size[i],

seed = 123

)

# 並將每一此訓練模型的OOB RMSE萃取儲存

hyper_grid$OOB_RMSE[i]

}

# 我們將結果依序OOB_RMSE由小至大排列，取模型成效前十名印出

hyper_grid %>%

dplyr::arrange(OOB_RMSE) %>%

head(10)

##    mtry node_size sample_size OOB_RMSE
## 1    20         5         0.8 25918.20
## 2    20         3         0.8 25963.96
## 3    28         3         0.8 25997.78
## 4    22         5         0.8 26041.05
## 5    22         3         0.8 26050.63
## 6    20         7         0.8 26061.72
## 7    26         3         0.8 26069.40
## 8    28         5         0.8 26069.83
## 9    26         7         0.8 26075.71
## 10   20         9         0.8 26091.08

## mtry node_size sample_size OOB_RMSE

## 1 20 5 0.8 25918.20

## 2 20 3 0.8 25963.96

## 3 28 3 0.8 25997.78

## 4 22 5 0.8 26041.05

## 5 22 3 0.8 26050.63

## 6 20 7 0.8 26061.72

## 7 26 3 0.8 26069.40

## 8 28 5 0.8 26069.83

## 9 26 7 0.8 26075.71

## 10 20 9 0.8 26091.08

從前十名模型成效結果我們可以發現：

OOB_RMSE大致落在26K左右。
最適mtry的值落在所有20~30範圍區間。表示mtry在此區間對於OOB_RMSE沒有太大影響。
最適最小節點觀察值數量大約落在3~5。
最適抽樣比例約為0.8。
表示抽樣比例高(~80%)和深度較長(葉節點觀測個數大小3~5)的隨機森林成效較好(OOB RMSE)。

調整變數型態

雖然我們已知random forests對於原始類別型變數處理效果是不錯的，我們還是進一步來試試將類別變數重新編碼為dummy variables是否能提升random forests的預測表現。

以下，我們使用dummyVars()函數將類別變數重新編碼為虛擬變數。

to_dum <- dummyVars(formula = ~., data = ames_train, fullRank = FALSE)

to_dum

原始類別預測變數(80)被轉換完後變成353個欄位。

ames_to_dum <- predict(to_dum, newdata = ames_train) %>% as.data.frame()

1	ames_to_dum % as.data.frame()

將資料名稱變成ranger相容的名稱。

names(ames_to_dum) <- make.names(names = names(ames_to_dum), allow_ = FALSE)

1	names(ames_to_dum)

建立hyperparameter grid。並將mtry的區間調整為更大範圍。並執行grid search。

hyper_grid_2 <- expand.grid(
  mtry = seq(50, 200, by = 25),
  node_size  = seq(3, 9, by = 2),
  sampe_size = c(.55, .632, .70, .80),
  OOB_RMSE  = 0
)

for(i in 1:nrow(hyper_grid_2)){
  model <- ranger(
    formula = Sale.Price ~.,
    data = ames_to_dum, 
    num.trees = 500, 
    mtry = hyper_grid_2$mtry[i],
    min.node.size = hyper_grid_2$node_size[i], 
    sample.fraction = hyper_grid_2$sampe_size[i],
    seed = 123
  )

  hyper_grid_2$OOB_RMSE[i] <- sqrt(model$prediction.error)
}

hyper_grid_2

mtry = seq(50, 200, by = 25),

node_size = seq(3, 9, by = 2),

sampe_size = c(.55, .632, .70, .80),

OOB_RMSE = 0

)

for(i in 1:nrow(hyper_grid_2)){

model

formula = Sale.Price ~.,

data = ames_to_dum,

num.trees = 500,

mtry = hyper_grid_2$mtry[i],

min.node.size = hyper_grid_2$node_size[i],

sample.fraction = hyper_grid_2$sampe_size[i],

seed = 123

)

hyper_grid_2$OOB_RMSE[i]

}

hyper_grid_2 %>% 
  dplyr::arrange(OOB_RMSE) %>% 
  head(10)

hyper_grid_2 %>%

dplyr::arrange(OOB_RMSE) %>%

head(10)

##    mtry node_size sampe_size OOB_RMSE
## 1    50         3        0.8 26981.17
## 2    75         3        0.8 27000.85
## 3    75         5        0.8 27040.55
## 4    75         7        0.8 27086.80
## 5    50         5        0.8 27113.23
## 6   125         3        0.8 27128.26
## 7   100         3        0.8 27131.08
## 8   125         5        0.8 27136.93
## 9   125         3        0.7 27155.03
## 10  200         3        0.8 27171.37

## mtry node_size sampe_size OOB_RMSE

## 1 50 3 0.8 26981.17

## 2 75 3 0.8 27000.85

## 3 75 5 0.8 27040.55

## 4 75 7 0.8 27086.80

## 5 50 5 0.8 27113.23

## 6 125 3 0.8 27128.26

## 7 100 3 0.8 27131.08

## 8 125 5 0.8 27136.93

## 9 125 3 0.7 27155.03

## 10 200 3 0.8 27171.37

由結果可分發線

OOB RMSE 落在27K左右，並沒有比類別變數重新編碼前的26K來得好。
將類別變數重新編碼成dummy variables是無法提升模型成效的。

所以到目前為至，最適的random forests模型參數分別為mtry = 20, node_size = 5, sample_size = 0.8。我們重複執行100次這個參數設定的模型，來計算此模型的error rate的期望值大小。

OOB_RMSE <- vector(mode = "numeric", length = 100)

for(i in 1:length(OOB_RMSE)){
  optimal_ranger <- ranger(
    formula         = Sale_Price ~ ., 
    data            = ames_train, 
    num.trees       = 500,
    mtry            = 20,
    min.node.size   = 5,
    sample.fraction = .8,
    importance      = 'impurity'
  )

  OOB_RMSE[i] <- sqrt(optimal_ranger$prediction.error)
}

hist(OOB_RMSE, breaks = 20)

OOB_RMSE

for(i in 1:length(OOB_RMSE)){

optimal_ranger

formula = Sale_Price ~ .,

data = ames_train,

num.trees = 500,

mtry = 20,

min.node.size = 5,

sample.fraction = .8,

importance = 'impurity'

)

OOB_RMSE[i]

}

hist(OOB_RMSE, breaks = 20)

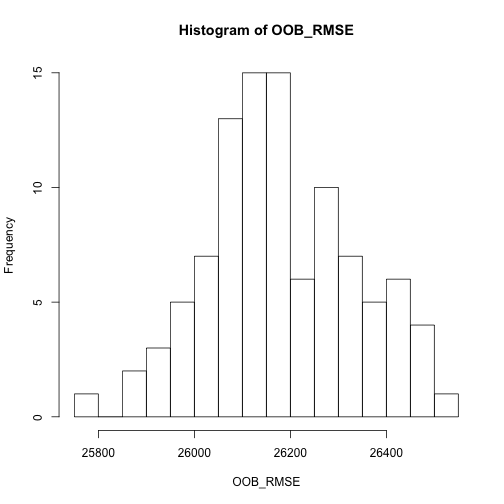
執行100次random forests的結果後，我們可以觀察到OOB RMSE的期望值約落在26000~26200區間。

另外，我們在在模型參數importance = ‘impurity’。這表示我們是依據節點不純度(node impurity)的改善幅度來衡量每個變數的重要性。變數的重要性是計算每一次使用不同變數切割結點後，總能使MSE下降的程度(跨多棵樹模型)，而那些無法透過該變數切割所降低的模型錯誤率，則被稱作node impurity。而能夠降低越多MSE的變數則被重要性越高。

因此，在每一次節點分割時，我們都會計算每個變數所造成的MSE下降程度，而累積下降MSE幅度最高者，則被認為是較為重要的變數。

我們將變數重要性結果繪出：

options(scipen = -1)
optimal_ranger$variable.importance %>% 
  as.matrix() %>% 
  as.data.frame() %>% 
  add_rownames() %>% 
  `colnames<-`(c("varname","imp")) %>%
  arrange(desc(imp)) %>% 
  top_n(25,wt = imp) %>% 
  ggplot(mapping = aes(x = reorder(varname, imp), y = imp)) +
  geom_col() +
  coord_flip() +
  ggtitle(label = "Top 25 important variables") +
  theme(
    axis.title = element_blank()
  )

options(scipen = -1)

optimal_ranger$variable.importance %>%

as.matrix() %>%

as.data.frame() %>%

add_rownames() %>%

`colnames%

arrange(desc(imp)) %>%

top_n(25,wt = imp) %>%

ggplot(mapping = aes(x = reorder(varname, imp), y = imp)) +

geom_col() +

coord_flip() +

ggtitle(label = "Top 25 important variables") +

theme(

axis.title = element_blank()

)

## Warning: Deprecated, use tibble::rownames_to_column() instead.

1 2	## Warning: Deprecated, use tibble::rownames_to_column() instead.

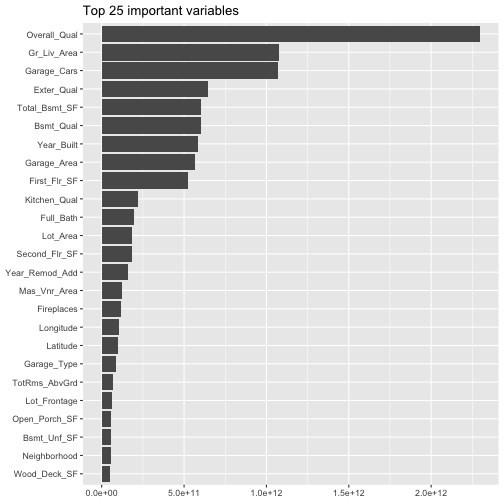
由上圖我們可以看到前三名重要變數依序為：Overall_Qual, Gr_Liv_Area, Garage_Cars。

Full grid search with H2O

我們已經知道剛剛在執行ranger進行hyperparameter grid計算時，還花滿長一段時間的。雖然ranger在計算上是有效率的，
但是當遇到大型的grid時，我們手寫的loop迴圈會變得非常沒有效率。

而這時候，h2o套件則是一個強大有效率的java-based介面，可以提供平行分布式運算方法。此外，h20還可以提供不同的”search path”。有別於一一執行每一種hyperparameter grid組合，h2o可允許不同的最適搜尋路徑來執行，直到模型成效改善達一定程度等search path。使得在tuning模型上更具效率。以下便來介紹如何使用h2o套件執行random forests。

# start up h2o
h2o.no_progress() # turn off progress bars when creating reports/tutorials)
h2o.init(max_mem_size = "4g")

# start up h2o

h2o.no_progress() # turn off progress bars when creating reports/tutorials)

h2o.init(max_mem_size = "4g")

##  Connection successful!
## 
## R is connected to the H2O cluster: 
##     H2O cluster uptime:         1 days 3 hours 
##     H2O cluster timezone:       Asia/Taipei 
##     H2O data parsing timezone:  UTC 
##     H2O cluster version:        3.22.1.1 
##     H2O cluster version age:    2 months and 19 days  
##     H2O cluster name:           H2O_started_from_R_peihsuan_qcx617 
##     H2O cluster total nodes:    1 
##     H2O cluster total memory:   0.04 GB 
##     H2O cluster total cores:    4 
##     H2O cluster allowed cores:  4 
##     H2O cluster healthy:        FALSE 
##     H2O Connection ip:          localhost 
##     H2O Connection port:        54321 
##     H2O Connection proxy:       NA 
##     H2O Internal Security:      FALSE 
##     H2O API Extensions:         XGBoost, Algos, AutoML, Core V3, Core V4 
##     R Version:                  R version 3.5.2 (2018-12-20)

## Connection successful!

## R is connected to the H2O cluster:

## H2O cluster uptime: 1 days 3 hours

## H2O cluster timezone: Asia/Taipei

## H2O data parsing timezone: UTC

## H2O cluster version: 3.22.1.1

## H2O cluster version age: 2 months and 19 days

## H2O cluster name: H2O_started_from_R_peihsuan_qcx617

## H2O cluster total nodes: 1

## H2O cluster total memory: 0.04 GB

## H2O cluster total cores: 4

## H2O cluster allowed cores: 4

## H2O cluster healthy: FALSE

## H2O Connection ip: localhost

## H2O Connection port: 54321

## H2O Connection proxy: NA

## H2O Internal Security: FALSE

## H2O API Extensions: XGBoost, Algos, AutoML, Core V3, Core V4

## R Version: R version 3.5.2 (2018-12-20)

首先我們先來使用完整grid search path (又叫做full cartesian)，即表示會逐一檢視所有我們所指派的參數組合(hyper_grid.h2o)。
根據hyper_grid.h2o的參數組合，共會有4*3*2 = 24種組合。也因為這邊是採用cartisian法，所以也不會比上面的方法快多少。

# create feature names
y <- "Sale_Price"
x <- setdiff(names(ames_train), y)

# turn training set into h2o object
train.h2o <- as.h2o(ames_train)

# create feature names

# turn training set into h2o object

train.h2o

# 指派參數組合 hyperparameter grid
hyper_grid.h2o <- list(
  ntrees      = seq(200, 500, by = 100),
  mtries      = seq(20, 25, by = 2),
  sample_rate = c(.70, .80)
)

# build grid search 
# 以「cartesian」法逐一執行每一個參數組合的隨機森林模型

# 測試24種組合所需的時間
system.time(
grid <- h2o.grid(
  algorithm = "randomForest",
  grid_id = "rf_grid",
  x = x, 
  y = y, 
  training_frame = train.h2o,
  hyper_params = hyper_grid.h2o,
  search_criteria = list(strategy = "Cartesian")
  )
)

# 指派參數組合 hyperparameter grid

hyper_grid.h2o

ntrees = seq(200, 500, by = 100),

mtries = seq(20, 25, by = 2),

sample_rate = c(.70, .80)

)

# build grid search

# 以「cartesian」法逐一執行每一個參數組合的隨機森林模型

# 測試24種組合所需的時間

system.time(

grid

algorithm = "randomForest",

grid_id = "rf_grid",

x = x,

y = y,

training_frame = train.h2o,

hyper_params = hyper_grid.h2o,

search_criteria = list(strategy = "Cartesian")

)

##   user  system elapsed 
##  9.628   3.104 874.954

1 2	## user system elapsed ## 9.628 3.104 874.954

# 蒐集結果並依照每一種參數組合模型的MSE誤差來排名
# collect the results and sort by our model performance metric of choice
grid_perf <- h2o.getGrid(
  grid_id = "rf_grid", 
  sort_by = "mse", 
  decreasing = FALSE
  )

# 蒐集結果並依照每一種參數組合模型的MSE誤差來排名

# collect the results and sort by our model performance metric of choice

grid_perf

grid_id = "rf_grid",

sort_by = "mse",

decreasing = FALSE

)

print(grid_perf)

1	print(grid_perf)

## H2O Grid Details
## ================
## 
## Grid ID: rf_grid 
## Used hyper parameters: 
##   -  mtries 
##   -  ntrees 
##   -  sample_rate 
## Number of models: 91 
## Number of failed models: 0 
## 
## Hyper-Parameter Search Summary: ordered by increasing mse
##   mtries ntrees sample_rate        model_ids                 mse
## 1     20    400         0.8 rf_grid_model_85 6.073124636667156E8
## 2     26    300         0.8 rf_grid_model_82 6.119220802095695E8
## 3     20    300         0.8 rf_grid_model_79 6.148210280053709E8
## 4     26    500         0.7 rf_grid_model_70 6.154919117655025E8
## 5     26    400         0.8 rf_grid_model_88 6.155747553830479E8
## 
## ---
##    mtries ntrees sample_rate        model_ids                 mse
## 86     24    200        0.55  rf_grid_model_3 6.629919566473577E8
## 87     28    200         0.7 rf_grid_model_53 6.643770708728626E8
## 88     28    300        0.55 rf_grid_model_11 6.644256979260525E8
## 89     30    200        0.55  rf_grid_model_6 6.658494098992392E8
## 90     22    500        0.55 rf_grid_model_20 6.755417850891622E8
## 91     28    200        0.55  rf_grid_model_5 6.786043491214715E8

## H2O Grid Details

## ================

## Grid ID: rf_grid

## Used hyper parameters:

## - mtries

## - ntrees

## - sample_rate

## Number of models: 91

## Number of failed models: 0

## Hyper-Parameter Search Summary: ordered by increasing mse

## mtries ntrees sample_rate model_ids mse

## 1 20 400 0.8 rf_grid_model_85 6.073124636667156E8

## 2 26 300 0.8 rf_grid_model_82 6.119220802095695E8

## 3 20 300 0.8 rf_grid_model_79 6.148210280053709E8

## 4 26 500 0.7 rf_grid_model_70 6.154919117655025E8

## 5 26 400 0.8 rf_grid_model_88 6.155747553830479E8

## ---

## mtries ntrees sample_rate model_ids mse

## 86 24 200 0.55 rf_grid_model_3 6.629919566473577E8

## 87 28 200 0.7 rf_grid_model_53 6.643770708728626E8

## 88 28 300 0.55 rf_grid_model_11 6.644256979260525E8

## 89 30 200 0.55 rf_grid_model_6 6.658494098992392E8

## 90 22 500 0.55 rf_grid_model_20 6.755417850891622E8

## 91 28 200 0.55 rf_grid_model_5 6.786043491214715E8

然而我們從上述結果可以注意到，最好的模型的OOB RMSE只有2.464371 × 10⁴ (<25K)，比我們先前所校正的模型效果都還更好。
這是由於h2o套件在參數包括「最小節點大小(minimum node size)」、「樹的深度(tree depth)」等都更「慷慨」，比如說h2o預設最小節點大小為1，而ranger和randomForest該參數則都預設為5。

Random Discrete grid search with H2O

當遇到參數變很多的情況下，額外增加一個參數將會巨幅拉大grid search執行時間。為了因應這樣的不變，h2o提供了一種叫做「RandomDiscrete」的grid search搜尋路徑，有別於「Cartisian」逐一執行所有組合，「RandomDiscrete」會隨機挑選參數組合，直到達到一定程度的改善幅度、或是超過一定的時間、或是已執行一定數目的模型數（或是以上三種情況的交叉組合）。雖然使用「RandomDiscrete」搜尋可能會錯過最佳的參數組合效果，但基本上他已經能夠調教出不錯的模型了。

比如說，以下範例的參數組同樣為24種，我們設計一個「RandomDiscrete」grid search，停止條件為達成以下任一條件：近10組模型的MSE相較於最佳模性的改善幅度未超過0.5%、執行時間超過600秒(30 min)。

# hyperparameter grid
hyper_grid.h2o <- list(
  ntrees      = seq(200, 500, by = 100),
  mtries      = seq(20, 25, by = 2),
  sample_rate = c(.70, .80)
)

# random grid search criteria
search_criteria <- list(
  strategy = "RandomDiscrete",
  stopping_metric = "mse",
  stopping_tolerance = 0.005,
  stopping_rounds = 10,
  max_runtime_secs = 30*60
  )


# build grid search 
system.time(
random_grid <- h2o.grid(
  algorithm = "randomForest",
  grid_id = "rf_grid2",
  x = x,
  y = y,
  training_frame = train.h2o,
  hyper_params = hyper_grid.h2o,
  search_criteria = search_criteria
  )
)

# hyperparameter grid

hyper_grid.h2o

ntrees = seq(200, 500, by = 100),

mtries = seq(20, 25, by = 2),

sample_rate = c(.70, .80)

)

# random grid search criteria

search_criteria

strategy = "RandomDiscrete",

stopping_metric = "mse",

stopping_tolerance = 0.005,

stopping_rounds = 10,

max_runtime_secs = 30*60

)

# build grid search

system.time(

random_grid

algorithm = "randomForest",

grid_id = "rf_grid2",

x = x,

y = y,

training_frame = train.h2o,

hyper_params = hyper_grid.h2o,

search_criteria = search_criteria

)

##  user  system elapsed 
##  6.721   1.877 713.918

## user system elapsed

## 6.721 1.877 713.918

# collect the results and sort by our model performance metric of choice
grid_perf2 <- h2o.getGrid(
  grid_id = "rf_grid2",
  sort_by = "mse",
  decreasing = FALSE
  )

# collect the results and sort by our model performance metric of choice

grid_perf2

grid_id = "rf_grid2",

sort_by = "mse",

decreasing = FALSE

)

print(grid_perf2)

1	print(grid_perf2)


H2O Grid Details
================

Grid ID: rf_grid2 
Used hyper parameters: 
  -  mtries 
  -  ntrees 
  -  sample_rate 
Number of models: 24 
Number of failed models: 0 

Hyper-Parameter Search Summary: ordered by increasing mse
  mtries ntrees sample_rate         model_ids                 mse
1     20    500         0.8 rf_grid2_model_19 5.996100879211967E8
2     22    500         0.8 rf_grid2_model_24  6.09073686599265E8
3     22    500         0.7  rf_grid2_model_4 6.096855932933546E8
4     24    400         0.8  rf_grid2_model_8 6.132880206896532E8
5     22    400         0.8 rf_grid2_model_13 6.151492899918578E8

---
   mtries ntrees sample_rate         model_ids                 mse
19     20    500         0.7 rf_grid2_model_12 6.347692770119294E8
20     22    300         0.7 rf_grid2_model_21 6.361713674445038E8
21     24    400         0.7  rf_grid2_model_6 6.431105576136292E8
22     20    400         0.7  rf_grid2_model_9   6.4353236575248E8
23     22    200         0.7  rf_grid2_model_5 6.477837564818393E8
24     24    200         0.8  rf_grid2_model_1  6.50234231493715E8

H2O Grid Details

================

Grid ID: rf_grid2

Used hyper parameters:

- mtries

- ntrees

- sample_rate

Number of models: 24

Number of failed models: 0

Hyper-Parameter Search Summary: ordered by increasing mse

mtries ntrees sample_rate model_ids mse

1 20 500 0.8 rf_grid2_model_19 5.996100879211967E8

2 22 500 0.8 rf_grid2_model_24 6.09073686599265E8

3 22 500 0.7 rf_grid2_model_4 6.096855932933546E8

4 24 400 0.8 rf_grid2_model_8 6.132880206896532E8

5 22 400 0.8 rf_grid2_model_13 6.151492899918578E8

---

mtries ntrees sample_rate model_ids mse

19 20 500 0.7 rf_grid2_model_12 6.347692770119294E8

20 22 300 0.7 rf_grid2_model_21 6.361713674445038E8

21 24 400 0.7 rf_grid2_model_6 6.431105576136292E8

22 20 400 0.7 rf_grid2_model_9 6.4353236575248E8

23 22 200 0.7 rf_grid2_model_5 6.477837564818393E8

24 24 200 0.8 rf_grid2_model_1 6.50234231493715E8

檢視「RandomDiscrete」grid search結果我們發現，經「隨機」檢視24組參數組合後，最佳的模型MSE只有2.448694 × 10⁴ (v.s. Cartisian grid search找到的2.464371 × 10⁴已非常接近)。且random discrete法只花了約11分鐘(=713/60)的時間(v.s. complete search的15分鐘(=874 sec / 60)。

一旦找到了最佳模型，我們就可以將模型套用在hold-out test set測試資料上來計算最後的「驗證誤差 test error」。結果顯示驗證RMSE誤差為23K，比elastic nets(32K)和bagging(36K)法低了$10K左右。

# 根據Cartesian法中，選出MSE最低的model，
# Grab the model_id for the top model, chosen by validation error
best_model_id <- grid_perf2@model_ids[[1]]
best_model <- h2o.getModel(best_model_id)

# 根據Cartesian法中，選出MSE最低的model，

# Grab the model_id for the top model, chosen by validation error

best_model_id

best_model

# Now let’s evaluate the model performance on a test set
ames_test.h2o <- as.h2o(ames_test)

1 2	# Now let’s evaluate the model performance on a test set ames_test.h2o

best_model_perf <- h2o.performance(model = best_model, newdata = ames_test.h2o)

1	best_model_perf

# RMSE of best model
h2o.mse(best_model_perf) %>% sqrt()

1 2	# RMSE of best model h2o.mse(best_model_perf) %>% sqrt()

## [1] 23303.05

1 2	## [1] 23303.05

預測

一但我們挑出了我們偏好的模型，就像之前一樣，可以使用predict()函數將模型套用在新的資料集上做預測。我們可以來比較所有模型類別的預測效果(randomForest, ranger, h2o)(隨然呈現的結果有稍稍的不一樣)。另外要注意的就是h2o模型使用資料的格式不太依樣。

randomForest

# randomForest
pred_randomForest <- predict(ames_randomForest, ames_test)
head(pred_randomForest)

# randomForest

pred_randomForest

head(pred_randomForest)

##        1        2        3        4        5        6 
## 128454.9 155459.6 264329.4 382519.7 211966.4 214173.0

## 1 2 3 4 5 6

## 128454.9 155459.6 264329.4 382519.7 211966.4 214173.0

ranger

# ranger
pred_ranger <- predict(ames_ranger, ames_test)
head(pred_ranger$predictions)

# ranger

pred_ranger

head(pred_ranger$predictions)

## [1] 128893.3 154095.1 270183.4 389106.2 222629.6 210352.8

1 2	## [1] 128893.3 154095.1 270183.4 389106.2 222629.6 210352.8

h2o

# h2o
pred_h2o <- predict(best_model, ames_test.h2o)

1 2	# h2o pred_h2o

head(pred_h2o)

1	head(pred_h2o)

##    predict
## 1 119430.6
## 2 152900.0
## 3 278208.3
## 4 283966.7
## 5 225166.7
## 6 200583.3

## predict

## 1 119430.6

## 2 152900.0

## 3 278208.3

## 4 283966.7

## 5 225166.7

## 6 200583.3

小結

random forest是一個非常強大的「開箱即用」的演算法。不用太多的參數調教就會有相當不錯的預測能力。
此外，random forest也是模型中對資料前處理要求最少的模型，不太需要做資料轉換，是許多解決預測問題時最快能應用的方法。
以bagging為基礎，並透過(1)每棵樹進行bootstrapped sample 與 (2)節點分割時隨機挑選變數清單來「去除樹模型間的相關性」，能有效提升模型的高變異性與提升預測精準度。

參考文章連結：

隨機森林 random forest

更多Decision Tree相關的統計學習筆記：

Gradient Boosting Machines GBM | gbm, xgboost, h2o | R語言

Decision Tree 決策樹 | CART, Conditional Inference Tree, RandomForest

Regression Tree | 迴歸樹, Bagging, Bootstrap Aggregation | R語言

Tree Surrogate | Tree Surrogate Variables in CART | R 統計

更多Regression相關統計學習筆記：

Linear Regression | 線性迴歸模型 | using AirQuality Dataset

Logistic Regression 羅吉斯迴歸 | part1 – 資料探勘與處理 | 統計 R語言

Logistic Regression 羅吉斯迴歸 | part2 – 模型建置、診斷與比較 | R語言

Regularized Regression | 正規化迴歸 – Ridge, Lasso, Elastic Net | R語言