有別於「分類」樹(classification tree)是用來找尋「最能區分標籤資料類別」的一系列變數,「迴歸」樹(regression tree)則是用來找尋「最能區分目標連續變數相近度」的一系列變數。迴歸樹投入變數可以式任何資料型態(與分類樹一樣),唯一差別是迴歸樹的目標變數是連續型變數。
不管是哪種型態的決策樹,單一決策樹模型的結果不穩定度高(high variance),預測能力也較弱,也因此我們多半會搭配使用bootstrap aggregating(or Bagging)(一種集成學習法ensemble learning),綜合多顆決策樹的預測結果,降低單一決策樹的變異度或不穩定性,避免overfitting過度配適的問題。而諸多更複雜的決策數模型也是由此衍伸,如隨機森林(Random Forest)和(Gradient Boosting Machine)。
而此篇學習筆記將會實作Regression Tree以及bagging。
Regression Tree
載入實作所需的套件
其中決策樹模型會使用到的套件就是rpart(分類決策樹也是使用該套件)。
|
1 2 3 4 5 6 |
library(rsample) # data splitting library(dplyr) # data wrangling library(rpart) # performing regression trees library(rpart.plot) # plotting regression trees library(ipred) # bagging library(caret) # bagging |
而範例資料則是使用AmesHousing package中的Ames Housing數據。
將資料分成70%訓練集,30%測試集:
|
1 2 3 4 |
set.seed(123) ames_split ames_train ames_test |
決定切點 (Deciding on splits)
- 決策樹的分枝演算法會由上而下進行,貪心的切割出最完整的樹。而每一個分裂點的選取,都會去檢視每一個投入變數的值切分的結果,找出使得切分後兩群(R1, R2)的組內誤差平方和(SSE, sums of squares error)最小的變數和切點。目標函示如下:
\[minimize\space \bigg\{SSE = \sum_{i \in R1}(y_{i} – c_{1})^2 + \sum_{i \in R2}(y_{i} – c_{2})^2 \bigg\}\] - 分枝演算法會反覆在各個切分後的子群聚中執行,直到達到停止切割的條件。
- 而這一棵經過貪心分枝結果的決策樹,會長的非常大,複雜度高。即便可能可以很好的預測訓練資料集,但很可能已過度配適(overfit),當將預測規則套用在新資料集,預測能力不穩定度高。
Cost complexity criterion
為了優化決策樹在新資料上的預測能力穩定度,我們會需要在訓練結果的複雜度、深度與預測穩定度取得平衡。
要找到這樣的平衡,我們的方法就是先長出一棵完整和最複雜的樹,並加入樹的複雜度作為目標函式的懲罰因子(cost complexity parameter,\(\alpha\)),並以此為目標來修剪出最適的決策樹模型。加入懲罰因子限制是的目標函數如下:
\[minimize \bigg \{ SSE + \alpha |T| \bigg \}\]
其中,T代表的是決策樹的終端節點(Terminal nodes)數量,\(\alpha\)則為懲罰參數,cost complexity parameter。
在不同給定的懲罰參數\(\alpha\)值下,我們可以找出修剪後最小的一棵樹,使得使得上述加入懲罰限制式的懲罰誤差(penalized error)(\(SSE + \alpha |T|\))最小(the lowest penalized error)。(以上概念與regularized regression的懲罰限制式很像。)
懲罰參數越小,會傾向得到較大較複雜的修剪後決策樹,而懲罰參數越大,修剪後決策樹則會較小較精簡。
因此,上述加入懲罰的誤差目標函示可以確保說,樹繼續變複雜的前提就是SSE的下降幅度要高於複雜度的懲罰成本(cost complexity penalty)。
而要怎麼決定最適的懲罰參數(\(\alpha\)),我們會評估多組對應不同水準\(\alpha\)值的模型組合,並使用交叉驗證法來計算每一個\(\alpha\)值的交叉驗證誤差(cross-validated error, X-val error),來尋找使得交叉驗證誤差最小的的最適\(\alpha\)值(optimal \(\alpha\))和最適的決策樹子集合(optimal subtree)。
「交叉驗證誤差(X-Val error)」:
- 此處的「誤差」就是加入懲罰因子的「懲罰誤差」\(SSE + \alpha |T|\),只是是透過k-fold交叉驗證所計算出來的,所以亦稱做「交叉驗證誤差(X-val error)」。
- 也因為此誤差是計算在測試資料集與真實值的誤差,故亦可稱作Predicted Residual sum of squares(PRESS),跟SSE不太一樣,SSE是使用訓練資料本身來計算與真實資料的誤差,因此SSE通常會比PRESS來的小。
優缺點
迴歸樹的優點包括:
- 結果很好解釋。
- 可以快速產生預測規則(每一次分割只需找出最適的變數與切點,沒有太複雜的計算)。
- 可以從樹的長相與順序得知變數的重要性,越先被拿來切割的變數,該變數所能降低的SSE幅度越大。
- 如果模型預測途中遇到遺失值,雖然不能從上而下將該筆資料列分類,但我們可以在遇遺失值的節點處,由下而上取每個節點的平均值回溯估計該遺失值。
- 決策樹模型提供一個非線性的”jagged”(參差不齊的) response平面,所以他可以配適真實不是很平滑(smooth)的回歸平面。而如果真實回歸平面是平滑的,則片段的常數(piece-wise constant)可以任意逼近它。
- 存在許多快速、可靠的演算法來學習這些樹模型。
而迴歸樹的幾個缺點包括:
- 單一迴歸樹的變異數大,預測能力不穩定(使用訓練資料的子集合即能大大改變樹的末梢節點長相。)
- 也因為單一迴歸樹的變異數大,預測精準度也不太佳。
使用R來執行基本的迴歸樹演算法
我們可以使用rpart()來執行迴歸樹演算法,並使用rpart.plot()來繪製模型結果。方式大致與分類樹相同,唯一差別在於method參數要設定為”anova”。
|
1 2 3 4 5 |
m1 formula = Sale_Price ~ ., data = ames_train, method = "anova" ) |
我們可以執行m1來看一下模型訓練結果,會詳細說明每一次切割所使用的變數和切點,以及切割前後的資料筆數變化。
|
1 |
m1 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
## n= 2051 ## ## node), split, n, deviance, yval ## * denotes terminal node ## ## 1) root 2051 13299200000000 181620.20 ## 2) Overall_Qual=Very_Poor,Poor,Fair,Below_Average,Average,Above_Average,Good 1699 4001092000000 156147.10 ## 4) Neighborhood=North_Ames,Old_Town,Edwards,Sawyer,Mitchell,Brookside,Iowa_DOT_and_Rail_Road,South_and_West_of_Iowa_State_University,Meadow_Village,Briardale,Northpark_Villa,Blueste 1000 1298629000000 131787.90 ## 8) Overall_Qual=Very_Poor,Poor,Fair,Below_Average 195 173369900000 98238.33 * ## 9) Overall_Qual=Average,Above_Average,Good 805 852605100000 139914.80 ## 18) First_Flr_SF< 1150.5 553 302338400000 129936.80 * ## 19) First_Flr_SF>=1150.5 252 374390700000 161810.90 * ## 5) Neighborhood=College_Creek,Somerset,Northridge_Heights,Gilbert,Northwest_Ames,Sawyer_West,Crawford,Timberland,Northridge,Stone_Brook,Clear_Creek,Bloomington_Heights,Veenker,Green_Hills 699 1260199000000 190995.90 ## 10) Gr_Liv_Area< 1477.5 300 247261100000 164045.20 * ## 11) Gr_Liv_Area>=1477.5 399 631199000000 211259.60 ## 22) Total_Bsmt_SF< 1004.5 232 164042700000 192946.30 * ## 23) Total_Bsmt_SF>=1004.5 167 281257000000 236700.80 * ## 3) Overall_Qual=Very_Good,Excellent,Very_Excellent 352 2874510000000 304571.10 ## 6) Overall_Qual=Very_Good 254 885511300000 273369.50 ## 12) Gr_Liv_Area< 1959.5 155 325667700000 247662.30 * ## 13) Gr_Liv_Area>=1959.5 99 297033800000 313618.30 * ## 7) Overall_Qual=Excellent,Very_Excellent 98 1100817000000 385440.30 ## 14) Gr_Liv_Area< 1990 42 78801640000 325358.30 * ## 15) Gr_Liv_Area>=1990 56 756691700000 430501.80 ## 30) Neighborhood=College_Creek,Edwards,Timberland,Veenker 8 115305100000 281887.50 * ## 31) Neighborhood=Old_Town,Somerset,Northridge_Heights,Northridge,Stone_Brook 48 435248600000 455270.80 ## 62) Total_Bsmt_SF< 1433 12 31430660000 360094.20 * ## 63) Total_Bsmt_SF>=1433 36 258880600000 486996.40 * |
我們可以將上述模型結果用rpart.plot()函數來進行視覺化呈現。該函數參數可以進階調整圖形視覺畫呈現方式,可參考這篇文件。
|
1 |
rpart.plot(m1) |
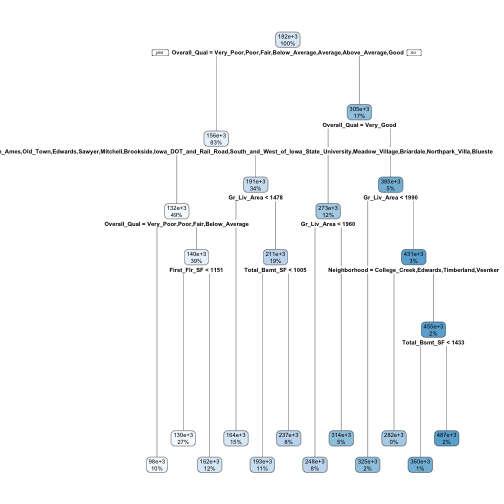
從上圖可以觀察到:
- 每一個節點的觀測值個數和目標變數平均值,顏色越深表示目標變數平均值越大。
- 該完整的決策樹共12個葉節點(leaf nodes or terminal nodes)以及11個內部節點(internal nodes)。
此外,我們也可以使用plotcp()函數,看一下在rpart()修樹過程中,套用不同懲罰參數(\(\alpha\))值,使用預設10-fold cross validation (k=10),計算hold-out資料與真實資料的誤差(懲罰誤差or交叉驗證誤差)變化圖。
|
1 |
plotcp(m1) |
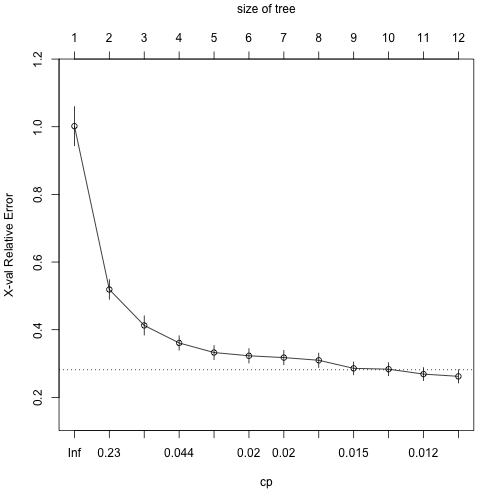
由上圖可以發現:
- 下x軸為cp or cost complexity parameter (\(\alpha\)),上x軸為末梢節點數(number of terminal nodes, |T|),y軸為交叉驗證誤差(X-val relative error)。
- 隨著懲罰係數減少,X-val error降低幅度呈遞減趨勢,直到cp達到預設的0.01則停止。
- 而根據專家建議,通常可以接受使用與最小X-val error相距一個標準差以內所對應的Tree Size(|T|)來作為修樹的最佳大小(1-SE rule)。比如說上圖中,水平虛線通過minimum X-val error – 1 SE的誤差值約對應在cp = 0.015和T = 9,因此我們亦可以選擇T = 9。
為了進一步說明為何要選擇T=12(或T=9 如果你採用 1 -SE rule)。我們可以將參數最小cp值設定為0,即沒有任何懲罰條件存在的狀況下,讓決策樹長到最大最完整。
|
1 2 3 4 5 6 7 8 9 |
m2 formula = Sale_Price ~ ., data = ames_train, method = "anova", control = list(cp = 0, xval = 10) ) {plotcp(m2) abline(v = 12,lty = "dashed", col = "red")} |
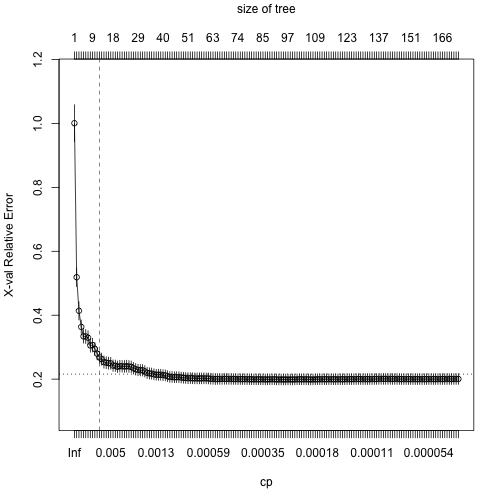
由上圖我們可以發現,當T>12後,即使樹繼續長大,但交叉驗證誤差下降幅度遞減,因此我們可以果斷將樹修剪到最精簡T=12且誤差也是最小的程度。
我們也可以看一下詳細的cp值和對應的X-Val error。rpart()預設的懲罰參數為cp=0.1,並執行一連串由大到小的\(\alpha\)值來計算誤差,直到cp=0.1所對應最小樹的大小為12(or 11 splits),最小交叉驗證誤差為0.262(xerror)。
|
1 |
m1$cptable |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
## CP nsplit rel error xerror xstd ## 1 0.48300624 0 1.0000000 1.0017486 0.05769371 ## 2 0.10844747 1 0.5169938 0.5189120 0.02898242 ## 3 0.06678458 2 0.4085463 0.4126655 0.02832854 ## 4 0.02870391 3 0.3417617 0.3608270 0.02123062 ## 5 0.02050153 4 0.3130578 0.3325157 0.02091087 ## 6 0.01995037 5 0.2925563 0.3228913 0.02127370 ## 7 0.01976132 6 0.2726059 0.3175645 0.02115401 ## 8 0.01550003 7 0.2528446 0.3096765 0.02117779 ## 9 0.01397824 8 0.2373446 0.2857729 0.01902451 ## 10 0.01322455 9 0.2233663 0.2833382 0.01936841 ## 11 0.01089820 10 0.2101418 0.2687777 0.01917474 ## 12 0.01000000 11 0.1992436 0.2621273 0.01957837 |
Tuning 修樹
除了使用懲罰參數cost complexity parameter (\(\alpha\))來限制樹的大小,我們也常透過以下參數來修樹:
- minsplit : 分裂前至少/最小所需的資料筆數。預設為20筆。如果將此數值調小,可讓末梢節點(terminal nodes)即使僅有少數一些資料,也可以產生對應的預測值。
- maxdepth : 從根節點(root nodes)到葉節點(terminal nodes)間的最大內部節點數量上限。預設為30,可以長出還滿大一棵樹。
rpart()函數中,是使用control這個參數來設定一系列的參數水準值(hyperparameter setting)。
比如說,我們想要建立一顆minsplit = 10和maxdepth = 12的決策樹模型。可以透過以下方式:
|
1 2 3 4 5 6 7 |
m3 rpart(formula = Sale_Price ~ ., data = ames_train, method = "anova", control = list(minsplit = 10, maxdepth = 12, xval = 10)) m3$cptable |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
## CP nsplit rel error xerror xstd ## 1 0.48300624 0 1.0000000 1.0007911 0.05768347 ## 2 0.10844747 1 0.5169938 0.5192042 0.02900726 ## 3 0.06678458 2 0.4085463 0.4140423 0.02835387 ## 4 0.02870391 3 0.3417617 0.3556013 0.02106960 ## 5 0.02050153 4 0.3130578 0.3251197 0.02071312 ## 6 0.01995037 5 0.2925563 0.3151983 0.02095032 ## 7 0.01976132 6 0.2726059 0.3106164 0.02101621 ## 8 0.01550003 7 0.2528446 0.2913458 0.01983930 ## 9 0.01397824 8 0.2373446 0.2750055 0.01725564 ## 10 0.01322455 9 0.2233663 0.2677136 0.01714828 ## 11 0.01089820 10 0.2101418 0.2506827 0.01561141 ## 12 0.01000000 11 0.1992436 0.2480154 0.01583340 |
雖然這個參數設定的方法挺管用,但如果想要評估不同參數水準組合的模型效果,手動調整就不具效率,此時,可以使用grid search的方法,來自動執行與比較不同參數水準值組合的效果並依據此來選擇最適合的模型參數設定。
執行grid search之前,我們先建立一個hyperparameter grid。舉例來說,想測試minsplit落在5-20區間和maxdepth落在8~15之間的參數組合(因為原始模型顯示最是模型節點數目為12)。這樣一來總共就會有16*8=128種參數組合的模型。
|
1 2 3 4 5 6 |
# 建立grid hyper_grid minsplit = seq(5,20,1), maxdepth = seq(8,15,1) ) head(hyper_grid) |
|
1 2 3 4 5 6 7 8 |
## minsplit maxdepth ## 1 5 8 ## 2 6 8 ## 3 7 8 ## 4 8 8 ## 5 9 8 ## 6 10 8 |
來看grid中的總共組合數。
|
1 |
nrow(hyper_grid) |
|
1 2 |
## [1] 128 |
接著使用loop迴圈來一一建立這128種不同參數組合的模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
models for(i in 1:nrow(hyper_grid)){ minsplit maxdepth models[[i]] formula = Sale_Price ~., data = ames_train, method = "anova", control = list(minsplit = minsplit, maxdepth = maxdepth) ) } |
接著,我們在撰寫一個函式來將每一組模型的最小交叉驗證誤差(x-val error)和對應的\(\alpha\)值取出,加到grid的資料集中。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# create the function to extract minimum error and associated alpha # get CP get_cp min cp } get_min_error min xerror } # 新增每組cp產生模型的cp和minXerror兩個欄位,並依照交叉驗證誤差由小到大排列,取前五個組合 hyper_grid %>% mutate( cp = purrr::map_dbl(models,get_cp), error = purrr::map_dbl(models,get_min_error) ) %>% arrange(error) %>% top_n(-5, wt = error) |
|
1 2 3 4 5 6 7 |
## minsplit maxdepth cp error ## 1 5 13 0.0108982 0.2421256 ## 2 6 8 0.0100000 0.2453631 ## 3 12 10 0.0100000 0.2454067 ## 4 8 13 0.0100000 0.2459588 ## 5 19 9 0.0100000 0.2460173 |
可發現hyperparameter參數組選出的最適模型的交叉驗證誤差較原始模型改善了一些(m1 的最小交叉驗證誤差 0.262 v.s. 最適模型的 0.242)。
我們將這組得到最小交叉誤差的模型套用在test data進行預測。
|
1 2 3 4 5 6 7 8 9 |
optimal_tree formula = Sale_Price ~ ., data = ames_train, method = "anova", control = list(minsplit = 5, maxdepth = 13, cp = 0.01) ) pred RMSE(pred = pred, obs = ames_test$Sale_Price) |
|
1 2 |
## [1] 39145.39 |
我們預測的Root-Mean-Squared-Error 平均誤差平方和開根號(均方根誤差)為39145。
Bagging
Bagging概念介紹
就像之前提到的,單一棵決策樹有變異度高(high variance)的問題。雖然修剪樹規則可以降低變異度,但其實有更有效的方法來大副降低變異度並提升決策樹的預測效果,其中一個方法就是Boostrap Aggregation (或稱Bagging)(概念來自於 Breiman, 1996)。
Bagging整合和平均多組模型的預測結果。透過平均每組模型的預測結果,
可以有效降低來自單一模型的變異度,並且避免過度配適overfitting。基本上Bagging可以分為三個基本步驟:
- 從訓練資料集(training data)中產生m組 bootstrap samples。Bootstrapped sample可以讓我們創造出有些差異的資料集,且這些資料集都是與原始訓練資料擁有相同分佈的。
- 對每一個bootstrapped sample訓練一組單一且未修剪的決策樹。
- 將每一組模型的結果平均,產生一個整體平均的預測值。
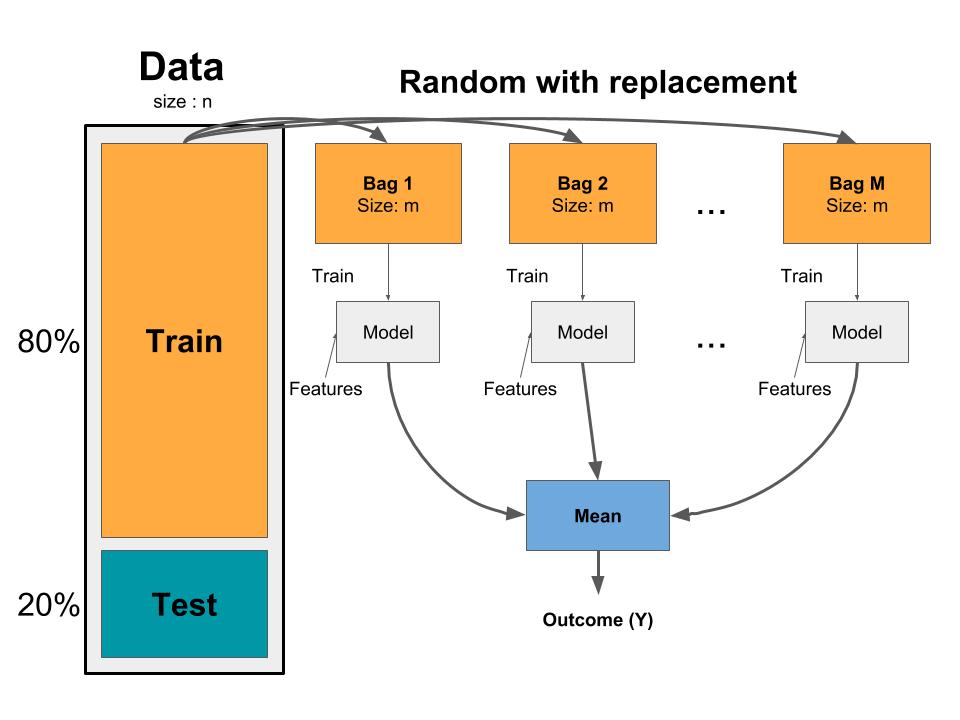
Bagging的概念可以套用在任何回歸和分類模型上;然而Bagging主要還是對於具有高變異度的模型較有效果。比如說,較為穩定的有母數模型(parametric model)如線性回歸和multi-adaptive regression splines模型,使用Bagging所能改善的預測能力幅度都較小。
Bagging的一個好處為,平均來說,一個Bootstrap sample會包含63%(2/3)的訓練資料集,剩餘約33%(1/3)的訓練資料不再bootstrapped sample內。我們稱這一包不在bootstrapped sample內的資料為out-of-bag (OOB) sample。我們可以透過這個OOB sample來衡量模型的準確度,產生一個自然而然的交叉驗證過程。
Bagging with ipred
配飾bagged tree model是簡單的。我們改使用ipred::bagging來建立模型。並將參數coob設定為TRUE來表示我們將使用OOB sample來估計模型錯誤率。
|
1 2 3 4 5 6 7 8 9 10 |
# make bootstrapping reproducible set.seed(123) bagged_m1 formula = Sale_Price ~ ., data = ames_train, coob = TRUE ) bagged_m1 |
|
1 2 3 4 5 6 7 8 |
## ## Bagging regression trees with 25 bootstrap replications ## ## Call: bagging.data.frame(formula = Sale_Price ~ ., data = ames_train, ## coob = TRUE) ## ## Out-of-bag estimate of root mean squared error: 36543.37 |
我們可以發現,經由bagged後的決策數模型錯誤率將近下降了快2602(from 39145 to 36543)。
需要注意的一點就是,一般來說,越多樹模型效果越好。當我們加入更多樹模型,就可以平均更多高變異度的單一樹模型。隨著模型的數量增加,我們可以得到大幅降低的變異度(以及錯誤率),並且直到某一數量水準值為止,變異度下降的幅度開始趨緩收斂,即可得到建立穩定模型所需的最適的樹數量。從經驗上來說,通常不太會用到超過50棵樹來穩定模型的誤差。
bagging預設會產生25組bootstrap sample和樹模型,但有時候我們可能需要更多顆樹模型。我們可以觀察樹的多寡和誤差的變化。我們觀察10~50棵樹在穩定模型誤差的效果變化。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# assess 10-50 bagged trees ntree # create empty vector to store OOB RMSE values rmse for(i in seq_along(ntree)){ # reproducibility: 固定bootstrap亂數結果 set.seed(123) # perform bagged model model formula = Sale_Price ~., data = ames_train, coob = TRUE, nbagg = ntree[i] ) # get OOB error rmse[i] } # 將不同樹數量與誤差的圖繪出 {plot(x = ntree, y = rmse,type = "l",lwd = 2) abline(v = 25, col = "red", lty = "dashed")} |
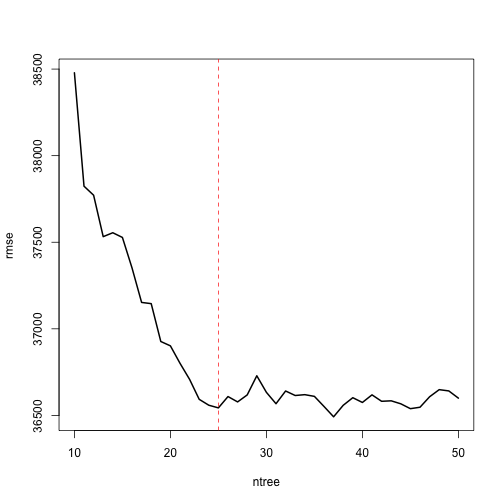
我們可以發現差不多在樹數量為25時誤差水準趨於穩定。所以如果單純僅加入更多樹不太能在優化模型的錯誤率。
Bagging with caret
使用ipred::bagging來進行bagging是簡單的,但使用caret來進行bagging會有更多好處如下:
- 他可以更簡單的進行cross validation。雖然我們可以使用OOB error,但使用cross validation可以提供強大的真實test error的誤差期望值。
- 我們可以跨多個bagged trees來衡量變數的重要性。
我們來建立一個10-fold cross validation的模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# Specify 10-fold cross validation ctrl # CV bagged model bagged_cv Sale_Price ~., data = ames_train, method = "treebag", trControl = ctrl, importance = TRUE ) # assess result bagged_cv |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
## Bagged CART ## ## 2051 samples ## 80 predictor ## ## No pre-processing ## Resampling: Cross-Validated (10 fold) ## Summary of sample sizes: 1846, 1845, 1847, 1845, 1846, 1847, ... ## Resampling results: ## ## RMSE Rsquared MAE ## 36477.25 0.8001783 24059.85 |
我們看到,交叉驗證的RMSE為36477。
我們亦可以看前20名重要變數分別為哪些。
|
1 2 |
# plot most important variables plot(varImp(bagged_cv),20) |
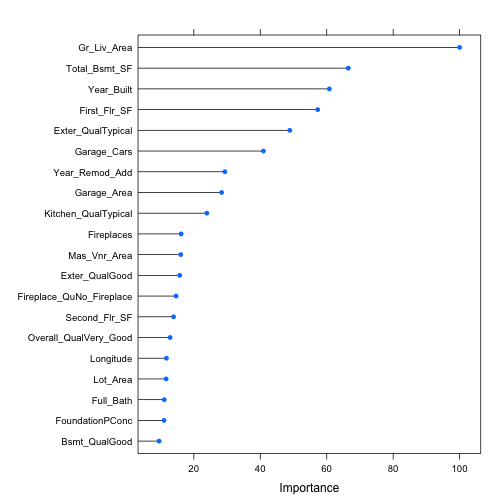
在回歸模型中,衡量變數的重要性為根據該變數切割(split)所能讓總SSE減少的量,並綜合平均m顆樹的效果。有最大影響SSE平均下降幅度的變數會被認為是最重要的變數。而上圖中重要性的值(importance value)則是每個變數平均使SSE下降程度相較於最重要變數的相對百分比(值的區間為0-100)。
同時,我們亦來比較將此模型套用在測試資料集的錯誤率(v.s. 交叉驗證錯誤率)。
|
1 2 |
pred RMSE(pred = pred,obs = ames_test$Sale_Price) |
|
1 2 |
## [1] 35262.59 |
可以發現cross validation(36477)和套用在test set(out of sample)的估計錯誤率(estimated error)(35263)是非常相近的。
而在之後的學習筆記中,會看從bagging概念所延伸的模型(如隨機森林Random Forest和GBMs)可以如何更好的改善模型錯誤率。
小結
- 決策樹是一個非常直覺的模型演算法,有許多好處,但卻有高變異度(high variance)的問題。雖然可以透過更改修剪樹的規則(如cp,minsplit,maxdepth)來改善誤差和過度配飾(overfitting),但程度有限。
- 能有效解決高變異度的問題可以透過Bagging(Bootstrap Aggregation)法,綜合和平均多棵樹模型的預測值,降低單一棵樹模型所產生的高變異度,並提升模型預側能力(降低錯誤率)。隨著樹的數量的增加,Bagging模型錯誤率會在某一最適值下趨於收斂與穩定。
- 評估Bagging模型錯誤率常用的方法可以是簡單的OOB error或是更強大的cross-validation error,兩者分別可以透過inpred::bagging和caret::train來得到。而caret::train 另外的好處就是可以計算出跨bagged tree所計算出來的變數重要性。
- Bagging的概念可以套用在任何回歸或分類演算法上,但對於本身就非常穩定的有母數模型如linear regression等效果就沒有這麼大。
- Bagging概念也是更複雜模強大模型如隨機森林(Random Forest)和Gradient Boosting Machines (GBMs)的延伸。
更多統計模型學習筆記:
- Linear Regression | 線性迴歸模型 | using AirQuality Dataset
- Regularized Regression | 正規化迴歸 – Ridge, Lasso, Elastic Net | R語言
- Logistic Regression 羅吉斯迴歸 | part1 – 資料探勘與處理 | 統計 R語言
- Logistic Regression 羅吉斯迴歸 | part2 – 模型建置、診斷與比較 | R語言
- Decision Tree 決策樹 | CART, Conditional Inference Tree, Random Forest
- Regression Tree | 迴歸樹, Bagging, Bootstrap Aggregation | R語言
- Random Forests 隨機森林 | randomForest, ranger, h2o | R語言
- Gradient Boosting Machines GBM | gbm, xgboost, h2o | R語言
- Hierarchical Clustering 階層式分群 | Clustering 資料分群 | R統計
- Partitional Clustering | 切割式分群 | Kmeans, Kmedoid | Clustering 資料分群
- Principal Components Analysis (PCA) | 主成份分析 | R 統計
參考連結: