j-kelly-brito-256889-unsplash
 程式與統計統計模型

Regularized Regression | 正規化迴歸 – Ridge, Lasso, Elastic Net | R語言

發表於 jamleecute

在線性回歸模型中，為了最佳化目標函式(最小化誤差平方和)，資料需符合許多假設，才能得到不偏回歸係數，使得模型變異量最低。可現實中數據非常可能有多個特徵變數，使得模型假設不成立而產生過度配適問題，這時則需透過正規化法(regularized regression)來控制回歸係數，藉此降低模型變異以及樣本外誤差。

Regularized Regression

載入實作所需的套件

資料準備：Data 使用 AmesHousing package中的 Ames Housing data

為何需要資料正規化(Regularization)?

我們知道，OLS(Ordinary Least Squares)最小平方和線性回歸的最佳化目標函式就是尋找一個平面，使得預測與實際值的誤差平方和(Sum of Squared Error, SSE)最小化（如下圖，紫色點代表實際觀測值，粉紅色為預測平面，黑色實線則表示實際與預測值得殘差）。

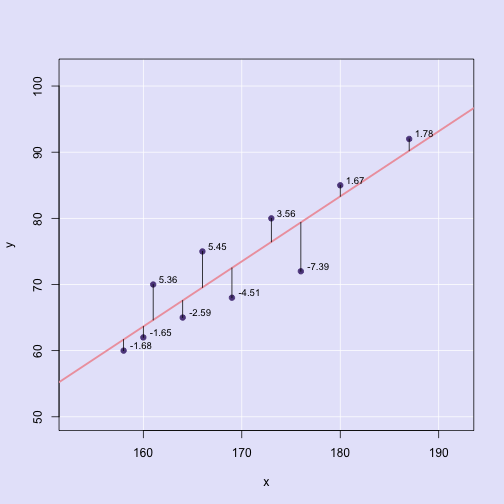
Regularized Regression

線性回歸的目標函式：

\[minimize\bigg \{ SSE = \sum_{i=1}^n (y_{i} – \hat{y}_{i})^2 \bigg \}\]

而要最佳化目標函式，資料必須符合以下幾個基本假設：

  • 線性關係
  • 變數成常態分配
  • 變數間無自相關
  • 殘差變異同質性
  • 觀測值個數(n)需大於特徵個數(p)(n>p)
  • 模型不能有共線性問題(否則估計回歸係數會有問題)

但現實中，數據往往存在許多特徵變數(p很大)，隨著特徵變數量增加，許多基本假設不再成立，以至於我們必須用替代方法來解決線性預測問題。具體來說，當特徵變數量增加(p增加)，我們常會遇到的三個主要問題包括：

1. Multicollinearity 多元共線性

當特徵變數個數增加(p增加)，我們就有越高的機會捕捉到存在共線性的變數。而當模型存在共線性時，回歸係數項就會變得非常不穩定(high variance, 高變異)。
舉例來說，我們先從多達81個特徵變數中:

  1. 找出相關係數絕對值高於0.6的變數組合。
  2. 找出哪些變數與自變數(Sale_Price)具有高度相關性(相關係數絕對值大於 0.6)。

首先我們先計算出每對變數間的相關係數和P-value的data frame

列出相關係數絕對值高於0.6的變數組合

列出與目標變數Sale_Price有高度相關(相關係數絕對值高於0.5)的變數組合

我們取具有高相關性的兩變數Gr_Liv_Area、TotRms_AbvGrd來說明。兩變數相關係數高達0.81。其中，Gr_Liv_Area和TotRms_AbvGrd皆分別與目標變數具有高度相關(相關係數分別為：cor = 0.71 and cor = 0.50)。

我們將兩變數投入線性模型進行配適，並比較各自投入線性回歸的係數。

模型1: 投入兩高相關性變數

模型2: 單獨使用Gr_Liv_Area進行回歸的結果。

模型3: 單獨使用TotRms_AbvGrd進行回歸的結果。

可以發現：

  • 兩高相關變數同時進行回歸配適時，會得到Gr_Liv_Area與目標變數為正相關而TotRms_AbvGrd與目標變數為負相關的係數結果。
  • 單獨投入回歸配適時，Gr_Liv_Area和TotRms_AbvGrd都變成正向係數。

以上係數正負號有問題的結果，就是模型存在共線性問題時常遇到的結果。具高度相關的變數係數會過度膨脹(over-inflated)且變得很不穩定(fluctuate significantly)。係數項大幅波動的結果，就是過度配適(overfitting)，也就是說，在權衡“bias-variance”(即誤差v.s模型變異度)階段中具模型有很高的變異度。雖然我們可以在建模後(事後)，使用VIF(variance inflation factors)變異數膨脹因子來檢查哪些變數有共線性並移除，但仍不太清楚要移除哪個變數好，或者是擔心移除變數會讓模型失去有價值的訊號。

2. Insufficient Solution 解決方案不充分

當特徵個數(p)超過觀測個數(n)(p>n)時，OLS(最小平方法)回歸解矩陣是不可逆的(solution matrix is not invertible)。這代表(1)最小平方估計參數解不是唯一。會存在無限的可用的解，但這些解大多都過度配適資料。(2)在大多數的情況下，這些結果在計算上是不可行的(computationally infeasible)。

因此，只能透過移除特徵變數直到(n>p)再將資料投入最小平方回歸模型進行配適。雖然可以透過人工的方式事前處理特徵變數過多的問題，但可能很麻煩且容易出錯。

3. Interpretability 可解釋性

當我們的特徵變數個數量很大時，我們會希望識別出具有最強解釋效果的較小子集合(Subsetting)。通常我們會偏好透過變數選取(feature selection)的方法來解決。其中一個變數選取法叫做「hard thresholding feature selection(硬閾值特徵選取)」，可以透過線性模型選取(linear model selection)來進行（best subsets & stepwise regression)，但這個方法通常計算上效率較低也不好擴展，而且是直接透過增加或減少特徵變數的方式來進行模型比較。另一個方法叫做「soft thresholding feature selection(軟閾值特徵選取)」，此法將慢慢的將特徵效果推向0。

Regularized Regression 正規化回歸

當遇到以上問題，一個替代OLS回歸的方法就是透過「正規化回歸 regularized regression」(又稱作penalized models或shrinkage method)來對回歸係數做管控。正規化回歸模型會對回歸係數大小做出約束，並逐漸的將回歸係數壓縮到零。而對回歸係數的限制將有助於降低係數的幅度和波動，並降低模型的變異。

正規化回歸的目標函式與OLS回歸類似，但多了一個懲罰參數(penalty parameter, P)：

\[minimize\bigg \{ SSE + P \bigg \}\]

而常見的懲罰係數有兩種(分別對應到ridge回歸模型 & lasso回歸模型)，效果是類似的。懲罰係數將會限制回歸係數的大小，除非該變數可以使誤差平方和(SSE)降低對應水準，該特徵係數才會上升。以下就來進一步介紹兩種最常見的正規化回歸法。

Ridge Regression

Ridge Regression透過將懲罰參數\(\lambda \sum_{j=1}^p \beta_{j}^2\)加入目標函式中。也因為該參數為對係數做出二階懲罰，故又稱為L2 Penalty懲罰參數。

\[minimize\bigg \{ SSE +\lambda \sum_{j=1}^p \beta_{j}^2 \bigg \}\]

而L2懲罰參數的值可以透過「tuninig parameter, \(\lambda\)」來控制。當\(\lambda \rightarrow 0\)，L2懲罰參數就跟OLS回歸一樣，目標函式只有最小化SSE；而當\(\lambda \rightarrow \infty\)時，懲罰效果最大，迫使所有係數都趨近於0。(如下圖範例所示，係數隨著\(\lambda\)由0變化到821(log(821) = 6.7)，係數逐漸被ridge法正規化的過程。)

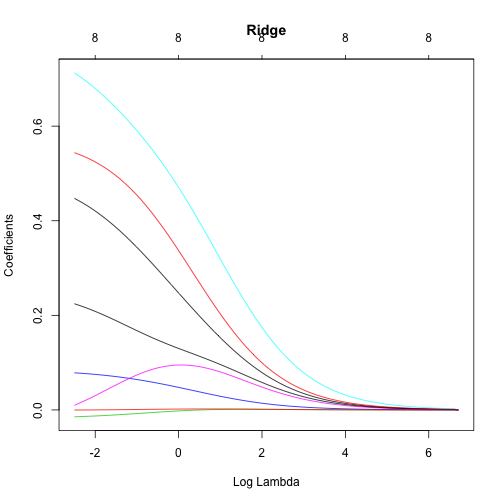
Regularized Regression, Ridge

由上圖我們可以觀察到：

  • 部分特徵係數會波動，直到\(\log(\lambda) \simeq 0\)才逐漸穩定開始收斂至0。這表示存在多重共線性，唯有透過\(\log(\lambda) > 0\)校正參數來限制係數，以降低模型變異和誤差。

但如何決定最適的shrinkage的程度(校正參數\(\lambda\))來最小化模型誤差呢？我們會透過以下的R程式語言實作來說明。

實作ridge regression using R

這邊主要會使用glmnet套件來執行。因為glmnet函數沒使用formula參數，故我們需要將資料分成x和y來帶入glmnet函數參數值，且x參數須為matrix型態。而我們將會使用model.matrix()函數來將質性變數轉換成dummy variables虛擬變量（如果資料維度很大的時候，則可參考更有效率的處理函數 Matrix::sparse.model.matrix）(並將第一行的截距項忽略)。另外，我們也將目標變數進行log轉換(因為目標變數分佈有偏)。

step 1: 將資料分成預測變數矩陣與目標變數，並替目標變數進行log轉換

查看質化變數經轉換成虛擬變量後，我們特徵變數維度從原始81個維度，增加為307個維度（不含截距項）。

step 2: 執行ridge model

我們使用glmnet::glmnet()來建立Ridge模型，並使用參數alpha來指定說要使用哪種懲罰參數，alpha = 0為Ridge，alpha = 1為lasso，或是 0 \(\leq\) alpha \(\leq\) 1為elastic net。

glmnet會在執行時，主要會做兩件事：

  1. 預測變數在投入正規化回歸模型(regularized regression)前是需要被標準化(standardized)。而glmnet函數則會幫你處理標準化這件事。如果你已在使用glmnet前標準化預測變數，則可將參數設定為standaradize = FALSE。
  2. glmnet會跨非常大的\(\lambda\)區間來執行ridge model。如下圖所示：

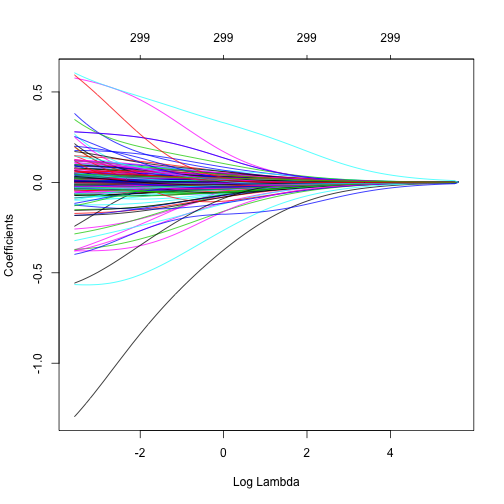
Regularized Regression, Ridge

我們可以用以下方式看\(\lambda\)的區間。glmnet預設為使用100組\(\lambda\)，當然你也可以自行指定\(\lambda\)區間，但絕大多數時候是不太需要去調整的。

我們亦可透過coef()函數去查看每個\(\lambda\)懲罰係數模型產生的係數。glmnet會儲存每個模型的所有係數，並按照\(\lambda\)由大到小排列。
但由於預測變數實在太多，我們只挑Gr_Liv_Area和TotRms_AbvGrd兩個變數分別在\(lamda\)為最大(279.1034874)和最小值(0.0279103)的係數值。

對應到最小\(\lambda\)值的係數。

對應到最大\(\lambda\)值的係數。可以看到當\(\lambda\)懲罰係數很大時，係數幾乎都被壓縮逼近到0。

雖然看到了懲罰係數\(\lambda\)對係數限制的效果，但到目前為止我們還不了解懲罰限制式對模型的改善程度。

Tuning

\(\lambda\)是一個用來校正參數，用來避免模型對訓練資料集產生過度配適的情況。然而，為了找出最適的\(\lambda\)，我們會需要利用cross-validation來協助。我們可以透過cv.glmnet()函數來執行k-fold cross validation，預設k=10。

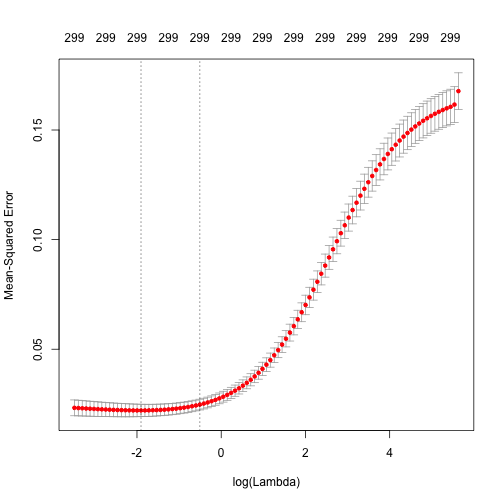
Regularized Regression, Ridge

上圖為執行10-fold cross validation，不同\(\lambda\)值所對應的MSE(mean squared error)的結果。我們可以就MSE變化的區間發現，其實改善幅度有限；但是我們發現，當我們對係數使用\(\log(\lambda) \geq 0\)的懲罰係數，則MSE就會大幅上升。圖上方的數字(299)表示模型中的變數數目。因為Ridge Model不會直接強制讓變數係數變成0，所以模型中的變數數目維持不變。(但在lasso和elastic模型中就不大一樣)。

圖中的第一和第二條垂直虛線則分別代表：

  • 對應最小MSE的\(\lambda\)
  • 對應最小MSE一個標準差內的最大\(\lambda\)

我們可以透過以下指令查看兩者的值：

最小MSE值

對應最小MSE的\(\lambda\)

對應最小MSE的\(\log(\lambda)\)

距離最小MSE一個標準差內的MSE值

對應距離最小MSE一個標準差內的\(\lambda\)

對應距離最小MSE一個標準差內的\(\log(\lambda)\)

在lasso和elastic模型中，使用對應距離最小MSE一個標準差內的\(\lambda\)是很明顯的結果。但在ridge模型中，我們可先用視覺化圖表來衡量。

我們將所有對應不同\(\lambda\)的係數值繪出，並以紅色垂直虛線表示對應最小MSE一個標準差內\(\lambda\)。

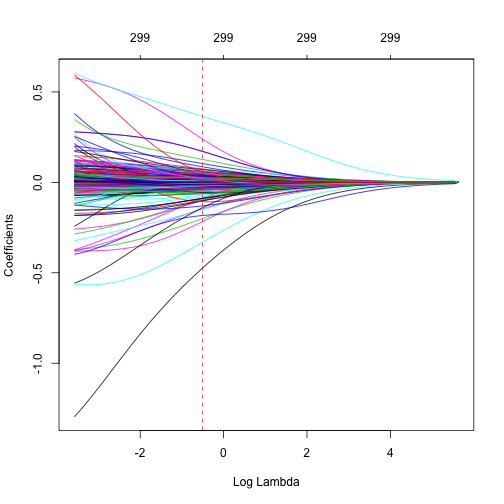
Regularized Regression, Ridge

由上圖我們可以看到，在極大化預測精準度的同時，我們可以對係數做出多少限制。

Advantages & Disadvantages

優點
  1. 實質上，Ridge模型會將具有相關性的變數推向彼此，並避免使得其中一個有極大正係數另一個有極大負係數的情況。
  2. 此外，許多不相干的變數係數會被逼近為0(不會等於0)。表示我們可以降低我們資料集中的雜訊，幫助我們更清楚的識別出模型中真正的訊號(signals)。

比如說以下我們來看對應\(\lambda\)值為最小MSE一個標準差的模型中，Top 25個具有影響力的變數分別有哪些。

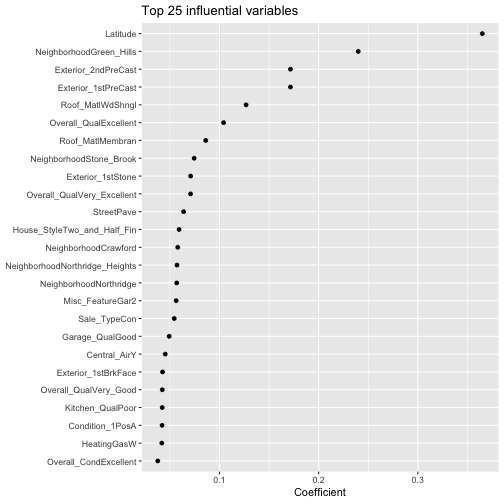
Regularized Regression, Ridge

缺點
  1. 然而，Ridge模型會保留所有變數。假如你覺得需要保留所有變數並將較無影響力的變數雜訊給減弱並最小化共線性，則模型是好的。
  2. Ridge 模型是不具有變數挑選(feature selection)功能的。假如妳需要更近一步減少資料中的訊號(signals)並尋找subset來解釋，則lasso模型會更適合。

Lasso Regression

Lasso的全名為Least absolute shrinkage and selection operator( Tibshirani, 1996)。是Ridge模型外的另一個選擇，並在目標函式的限制式有所調整。有別於二階懲罰(L2 Penalty)，Lasso模型在目標函式中所使用的是一階懲罰式(L1 Penalty)\(\lambda \sum_{j=1}^p |\beta_{j}|\)。

\[ minimize \bigg \{ SSE + \lambda \sum_{j=1}^p |\beta_{j}| \bigg\} \]

不像Ridge模型只會將係數逼近到接近零（但不會真的是0），Lasso模型則真的會將係數推進成0(如下圖)。因此，Lasso模型不僅能使用正規化(regulariztion)來優化模型，亦可以自動執行變數篩選(Feature selection)。

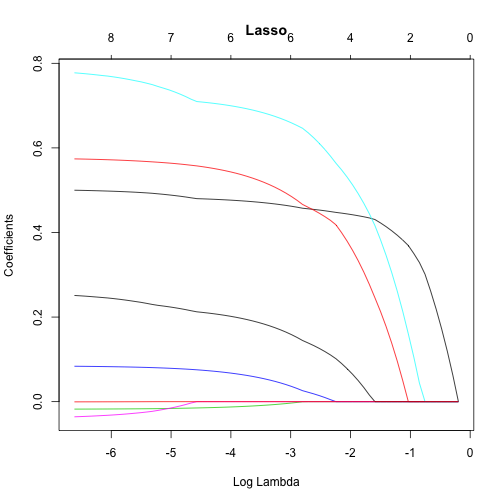
Regularized Regression, Lasso

從上圖我們可以看到，在\(\log(\lambda) = -6\)時，所有8個變數（圖表上方數字）都包還在模型內，而當在\(\log(\lambda) = -3\)時只剩下6個變數，最後當在\(\log(\lambda) = -1\)時，只剩2個變數被保留在模型內。因此，當遇到資料變數非常多時，Lasso模型是可以幫你識別並挑選出有最強（也最一致）訊號的變數。

使用R實作Lasso模型

建置Lasso模型的方法跟Ridge模型作法一樣，只需將glmnet()函數中alpha參數改設定為1。

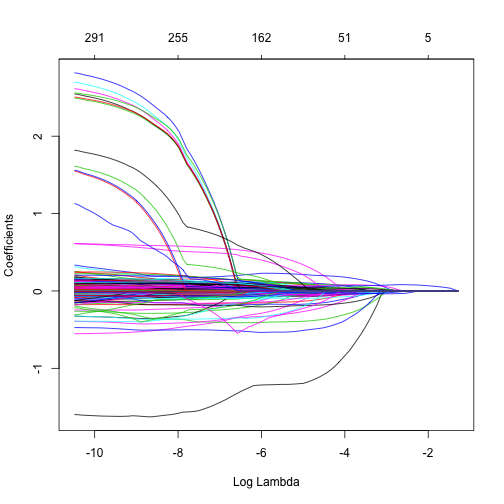
Regularized Regression, Lasso

從上圖中可以看到大約是在\(\log(\lambda) \rightarrow -6\)的時候，被保留在模型中的變數數目大量下降。而且，當\(\log(\lambda) = -10 \rightarrow \lambda = 0\)，在沒有懲罰限制式(跟OLS模型一樣)時，數個變數的係數值都非常大，表示可能變數與變數間存在高度相關而導致他們的係數變得極大。當我們對模型做出限制，這些資料中為雜訊的變數係數就會被推進成0。

同樣的，如何選擇最適的懲罰係數\(\lambda\)亦和Ridge模型一樣透過執行cross validation來看不同\(\lambda\)對應的MSE值，並找出使MSE發生最小值(或在一個標準差之內)的\(\lambda\)來決定。

Tuning

為了找出最適的\(\lambda\)，我們跟Ridge模型一樣，使用cv.glmnet()函數來看不同\(\lambda\)對應的MSE值，並將alpha參數設定為1。

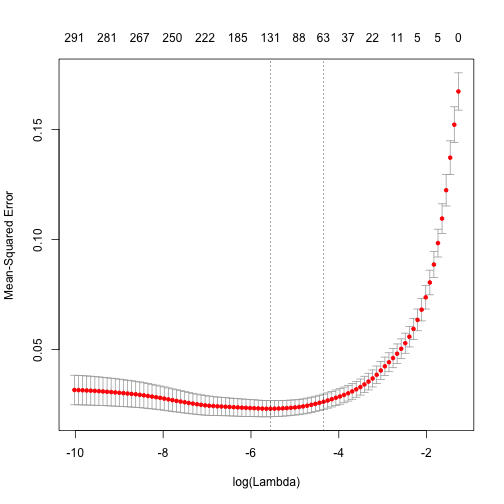
Regularized Regression, Lasso

從上圖可以發現，我們可以透過採用大約\( -6 \leq \log(\lambda) \leq -4\)的懲罰係數區間來最小化模型的MSE。而且在該懲罰係數區間，不僅最小化模型的MSE，同時也壓縮模型內被保留下來的變數數目至大約\(131 \geq p \geq 63\)的區間。

同樣的，我們可以透過以下方法來取得最小MSE和一個標準差內的MSE以及對應的\(\lambda\)。

minimum MSE

對應最小MSE的\(\log(\lambda)\)

within 1 S.E. of minimum MSE

對應到最小MSE一個標準差內的最大\(\log(\lambda)\)

此時在Lasso模型的例子中，使用對應到最小MSE一個標準差內的最大\(\lambda\)當作懲罰係數的優勢是更明顯的。假設我們使用對應最小MSE的\(\lambda\)當作懲罰係數，那麼我們可以將原始變數集個數從307降到小於150左右。但考量到MSE也會有些變化性(variability)，因此我們可以合理假設，可以使用稍微更高的懲罰係數來達成類似的MSE程度，其\(\lambda\)所對應的變數數目約為小於70的水準左右。如果你分析的目的志在說明與詮釋預測變數，這樣懲罰係數的選擇應會有很大的幫助。

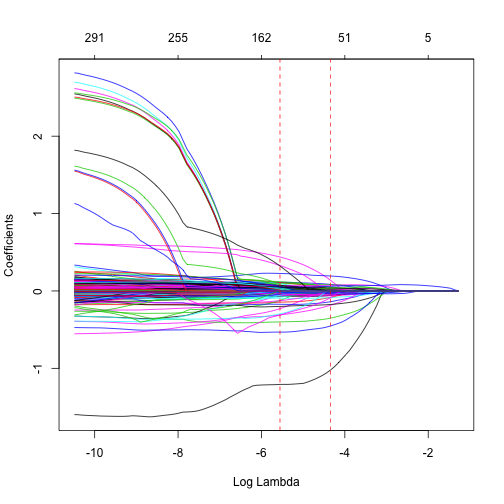
Regularized Regression, Lasso

Advantages and Disadvantages

優點
  1. 與Ridge模型一樣，Lasso模型亦會將具有相關性的變數推向彼此，並避免使得其中一個有極大正係數另一個有極大負係數的情況。
  2. 與Ridge模型最大的差別，就是Lasso會將不具影響力的變數係數變成0，自動進行變數篩選(Feature selection)。這樣的處理方式簡化並自動化識別出那些對模型預測正確性有高度影響力的變數。
缺點
  1. 然而，時常在我們移除變數的同時也會犧牲掉模型的正確性。所以為了得到Lasso產生的更清楚與簡潔的模型結果，我們也會降低模型的正確性。

一般來說，Ridge和Lasso模型所產生的最小MSE不會有太大差別(如下結果所示)。所以除非你單純只看最小化MSE的結果，實質上他們兩的差異並不顯著。

Elastic Net

涵蓋Ridge和Lasso兩個模型的就是Elastic Net模型(Zou and Hasie,005)，該模型綜合了兩個懲罰限制式。

\[ minimize \bigg \{ SSE + \lambda_{1} \sum_{j=1}^p \beta_{j}^2 + \lambda_{2} \sum_{j=1}^p |\beta_{j}| \bigg \} \]

雖然Lasso模型會執行變數挑選，但一個源自於懲罰參數的結果就是，通常當兩個高度相關的變數的係數在被逼近成為0的過程中，可能一個會完全變成0但另為一個仍保留在模型中。此外，這種一個在內、一個在外的處理方法不是很有系統。相對的，Ridge模型的懲罰參數就稍具效率一點，可以有系統的
將高相關性變數的係數一起降低。於是，Elastic Net模型的優勢就在於，它綜合了Ridge Penalty達到有效正規化優勢以及Lasso Penalty能夠進行變數挑選優勢。

使用R實作 Elastic Net

跟Ridge和Lasso一樣是使用glmnet()，並調整介於0~1之間的alpha參數。當alpha = 0.5時，Ridge和Lasso的組合是平均的，而當alpha\(\rightarrow\)0時，會有較多的Ridge Penalty權重，而當alpha\(\rightarrow\)1時，則會有較多的Lasso Penalty權重。

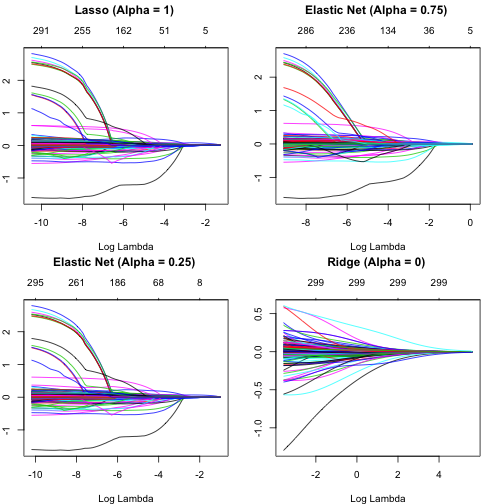
Regularized Regression, Elastic Net

tuning

在Ridge和Lasso模型中，\(\lambda\)是我們主要調整的參數，然而在Elastic Net模型中，我們會需要調教\(\lambda\)和alpha兩個參數。

首先，我們先建立一個fold_id，用來固定每一次建模每筆資料所在的fold id(1 ~ nfold)，即每次建模使用的CV folds都是相同的(如果單純只使用nfolds = 10，雖然每次建模都會進行10-fold的CV，但每一次資料所在的fold id卻是不一樣的)。(*在前的Ridge和Lasso的例子中，因為只會run一次CV.glmnet，來看不同\(\lambda\)值交叉驗證的MSE值，因此只需指定nfold數即可；但在Elastic Net模型中，會根據不同alpha(i.e., Ridge和Lasso權重佔比)來跑不同的cv.glmnet，為了確保模型結果不受亂數fold if結果影響，故固定每一次資料所在的fold id）

接著我們再建立一個tuning grid用來搜羅從0-1的區間的alpha值以及對應的空欄位值（包括最小MSE和一個標準差內的MSE以及兩者分別所對應的\(\lambda\)值）後續將用來儲存不同alpha參數跑出的CV模型結果。

接著，我們便可以開始迭代不同的alpha值(不同的Ridge & Lasso權重組成)，套用CV Elastic Net，萃取出每一個alpha值對應的模型結果，包括最小MSE以及一個標準差內的MSE、以及兩者分別所對應的\(\lambda\)值。

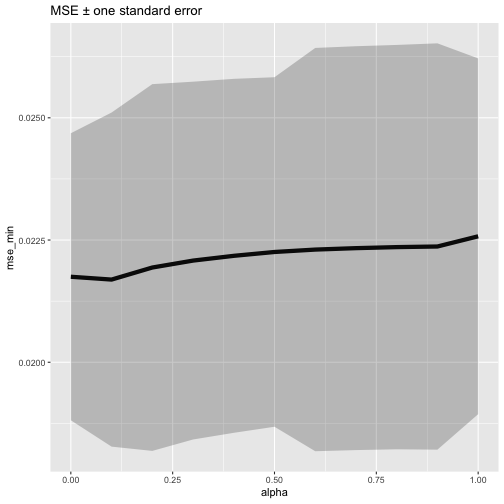
接著我們每一個alpha值跑出的模型中，最適\(\lambda\)值所對應的「最小MSE\(\pm\)1個標準差內的MSE區間」繪出，由下圖我們可以發現，
正負一個標準差內的MSE都落在相近的正確率區間(即不同alpha水準值間，模型正確率沒有太大差別)。因此，我們可以選取alpha = 1的Lasso模型來重重倚賴他的變數挑選功能，並合理假設模型正確率不會有損失(因為alpha從1變化到0正確率都沒有什麼變化)。

Regularized Regression, Elastic Net

優缺點

優點
  1. Elastic Model的優勢就是它綜合了Ridge Penalty的有效的正規化過程以及Lasso Penalty的變數篩選功能。讓我們能夠控制變數共線性的問題，能夠在p>n時執行回歸，並降低資料中過多的雜訊，以幫助我們將具有影響力的變數獨立出來且維持住模型正確率。
缺點
  1. 然而，Elastic Net，以及一般的regularization models，依舊有假設預測變數和目標變數需具有線性關係。雖然我們可以結合non-additive models(一種無母數回歸模型，non-parametric regression)交互作用，但當資料變數很多的時候，會是非常繁瑣與困難的。因此，當非線性關係存在時，可能考慮使用非線性迴歸的方法。

Predicting

一旦決定好最適的模型後，我們可以使用predict()函數，來將模型套用在新的資料集上做預測。唯一要注意的是，你需要提供predict()s參數，來指定你要的\(\lambda\)值。

比如說以下我們想要建立一個Lasso模型，並使用對應最小MSE的\(\lambda\)值來做預測。

我們預測結果的平均誤差平方為0.01483，比cv MSE的(0.02244)還來的更低些。

使用其他Package來實作: caret & h20

glmnet不是唯一能夠處理Regularized Regression的套件。常用的幾種套件包括caret和h20。以下僅簡單介紹caret套件的執行方法。

caret

小結

  1. 鑑於傳統一般線性回歸模型沒有挑選變數之功能，且又遇到變數特徵數量非常大的時候，會容易使得模型假設不成立並發生模型過度配適的問題（變異度高），為降低此變異和樣本外誤差，可以使用Regularized Regression。
  2. 常見的Regularized Regression方法包括，Ridge(alpha = 0)、Lasso(alpha=1)和Elastic Net(\(0\leq alpha \leq 1\))。他們分別透過二階的Ridge Penalty和一階的Lasso Penalty或綜合兩種Penalty(並以alpha設定Ridge & Lasso Penalty的權重)來對傳統OLS的目標函示的加上係數懲罰限制式，唯有該係數能夠降低的SSE幅度夠大才能增加其的係數大小。
  3. Ridge會有系統的將干擾變數係數逼近0(但不會等於0)，而Lasso則會將較無影響力的變數係數變成0。前者正規化過程較有效(即同為高度相關的變數，最終不會產生一個係數為零一個係數不為零的情況)，但從頭到尾都會保留模型中所有變數；後者則具有變數挑選的功能，但正規化過程較不具系統性。而Elastic Net則綜合上述兩者的優勢，同時兼顧有效的正規化過程以及變數挑選功能。
  4. 但不管是Ridge, Lasso還是Elastic Net，這些一般性線性回歸模型都收限於「預測變數需與目標變數成線性關係」之假設，若假設不成立，仍得考慮非線性的回歸模型。
  5. 此學習筆記僅介紹Regularized Regrssion的基本概念。Regularized Regression方法亦延伸出其他parametric generalized linear models（包括logistic regression, multinomial, poisson, support vector machines）。此外亦存在許多其他可替代方法如Least Angle Regression和The Bayesian Lasso。

更多統計學習筆記：

  1. Linear Regression | 線性迴歸模型 | using AirQuality Dataset
  2. Logistic Regression 羅吉斯迴歸 | part1 – 資料探勘與處理 | 統計 R語言
  3. Logistic Regression 羅吉斯迴歸 | part2 – 模型建置、診斷與比較 | R語言
  4. Decision Tree 決策樹 | CART, Conditional Inference Tree, Random Forest
  5. Regression Tree | 迴歸樹, Bagging, Bootstrap Aggregation | R語言
  6. Random Forests 隨機森林 | randomForest, ranger, h2o | R語言
  7. Gradient Boosting Machines GBM | gbm, xgboost, h2o | R語言
  8. Hierarchical Clustering 階層式分群 | Clustering 資料分群 | R統計
  9. Partitional Clustering | 切割式分群 | Kmeans, Kmedoid | Clustering 資料分群
  10. Principal Components Analysis (PCA) | 主成份分析 | R 統計

參考文章連結：

  1. 歐萊禮  R資料科學
  2. 正規化回歸 Regularized Regression
  3. R筆記 – (18) Subsets & Shrinkage Regression (Stepwise & Lasso)